Исследование функций при помощи производных
Теорема 1. (Ролль). Если функция  непрерывна на отрезке
непрерывна на отрезке  , дифференцируема на интервале
, дифференцируема на интервале  и на концах отрезка принимает одинаковые значения
и на концах отрезка принимает одинаковые значения 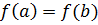 , то найдётся хотя бы одна точка
, то найдётся хотя бы одна точка  , в которой производная
, в которой производная  обращается в нуль, т.е.
обращается в нуль, т.е.  .
.
Так как функция  непрерывна на отрезке
непрерывна на отрезке  , то она достигает на этом отрезке своего наибольшего и наименьшего значений (по теореме Вейерштрасса), соответственно
, то она достигает на этом отрезке своего наибольшего и наименьшего значений (по теореме Вейерштрасса), соответственно  и
и  . Если
. Если  , то функция
, то функция  постоянна на
постоянна на  и, следовательно, её производная
и, следовательно, её производная  в любой точке отрезка
в любой точке отрезка  .
.
Если  , то функция достигает хотя бы одно из значений
, то функция достигает хотя бы одно из значений  или
или  во внутренней точке
во внутренней точке  интервала
интервала  , так как
, так как 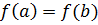 .
.

Геометрически теорема Ролля означает, что на графике функции  найдётся точка, в которой касательная к графику параллельна оси
найдётся точка, в которой касательная к графику параллельна оси  . Может быть и не одна такая точка, например, две.
. Может быть и не одна такая точка, например, две.
Теорема 2. (Коши). Если функции  и
и  непрерывны на отрезке
непрерывны на отрезке  , дифференцируемы на интервале
, дифференцируемы на интервале  , причём для
, причём для  для
для  , то найдётся хотя бы одна точка
, то найдётся хотя бы одна точка  такая, что выполняется равенство
такая, что выполняется равенство  .
.
Отметим, что  , так как в противном случае по теореме Ролля нашлась бы точка
, так как в противном случае по теореме Ролля нашлась бы точка  , такая, что
, такая, что  , чего не может быть по условия теоремы.
, чего не может быть по условия теоремы.
Теорема 3. (Лагранж). Если функция  непрерывна на отрезке
непрерывна на отрезке  , дифференцируема на интервале
, дифференцируема на интервале  , то найдётся хотя бы одна точка
, то найдётся хотя бы одна точка  такая, что выполняется равенство
такая, что выполняется равенство 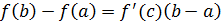 .
.
Эту формулу называют формулой Лагранжа или формулой о конечном приращении: приращение дифференцируемой функции на отрезке  равно приращению аргумента, умноженному на значение производной функции в некоторой внутренней точке этого отрезка.
равно приращению аргумента, умноженному на значение производной функции в некоторой внутренней точке этого отрезка.
Следствие 1. Если производная функции = 0 на некотором промежутке, то функция постоянна на этом промежутке.
Следствие 2. Если 2 функции имеют равные производные на некотором промежутке, то они отличаются друг от друга на постоянное слагаемое.
Теорема 4. (необходимые условия). Если дифференцируемая на интервале  функция
функция  возрастает (убывает), то
возрастает (убывает), то 
 для
для  .
.
Теорема 5. (достаточные условия). Если функция  дифференцируема на интервале
дифференцируема на интервале  и
и 
 для
для  , то эта функция возрастает (убывает) на интервале
, то эта функция возрастает (убывает) на интервале  .
.
Рассмотренные теоремы позволяют довольно просто исследовать функцию на монотонность.
Функция возрастающая или убывающая называется монотонной.
Пример. Исследовать функцию  на возрастание и убывание.
на возрастание и убывание.
Функция определена на  .
.
Её производная равна:  ;
;
 при
при  ;
;  при
при  .
.
 данная функция возрастает на интервалах
данная функция возрастает на интервалах 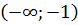 и
и  ; убывает на интервале
; убывает на интервале  .
.
Максимум и минимум функций.
Точка  называется точкой максимума функции
называется точкой максимума функции  , если
, если 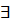 такая
такая  – окрестность точки
– окрестность точки  , что для всех
, что для всех 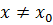 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство  .
.
Аналогично определяется точка минимума функции:  – точка минимума функции, если
– точка минимума функции, если
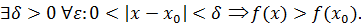
Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум (минимум) функции называется экстремумом функции.
Понятие экстремума всегда связано с определённой окрестностью точки из области определения функции. Поэтому функция может иметь экстремум лишь во внутренних точках области определения. Рассмотрим условия существования экстремума функции.
Теорема 6. (необходимое условие экстремума). Если дифференцируемая функция  имеет экстремум в точке
имеет экстремум в точке  , то её производная в этой точке равна нулю:
, то её производная в этой точке равна нулю:  .
.
 Геометрически равенство
Геометрически равенство
 означает, что в точке экстремума дифференцируемой функции
означает, что в точке экстремума дифференцируемой функции  касательная к её графику параллельна оси
касательная к её графику параллельна оси  .
.
 Обратная теорема неверна, т.е. если
Обратная теорема неверна, т.е. если  , то это не значит, что
, то это не значит, что  – точка экстремума.
– точка экстремума.
Например, для функции  её производная
её производная  равна нулю при
равна нулю при  , но
, но  не точка экстремума.
не точка экстремума.
 Существуют функции, которые в точках экстремума не имеют производной. Например, непрерывная функция
Существуют функции, которые в точках экстремума не имеют производной. Например, непрерывная функция  в точке
в точке  производной не имеет, но точка
производной не имеет, но точка  – точка минимума.
– точка минимума.
Таким образом, непрерывная функция может иметь экстремум лишь в точках, где производная функции равна нулю или не 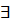 . Такие точки называют критическими.
. Такие точки называют критическими.
Теорема 7. (достаточное условие экстремума). Если непрерывная функция  дифференцируема в некоторой
дифференцируема в некоторой  – окрестности критической точки
– окрестности критической точки  и при переходе через неё (слева направо) производная
и при переходе через неё (слева направо) производная  меняет знак с плюса на минус, то
меняет знак с плюса на минус, то  есть точка максимума; с минуса на плюс, то
есть точка максимума; с минуса на плюс, то  – точка минимума.
– точка минимума.

Исследовать функцию на экстремум означает найти все её экстремумы.
Из приведённых теорем вытекает следующее правило исследования функции на экстремум:
1) найти критические точки функции  ;
;
2) выбрать из них лишь те, которые являются внутренними точками области определения функции;
3) исследовать знак производной  слева и справа от каждой из выбранных критических точек;
слева и справа от каждой из выбранных критических точек;
4) в соответствии с теоремой о достаточном условии экстремума, выписать точки экстремума (если они есть) и вычислить значения функции в них.
Пример. Найти экстремум функции 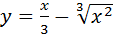 .
.
 . Находим
. Находим  , т.е.
, т.е.  .
.
Производная  при
при  и равна нулю при
и равна нулю при  . Эти точки разбивают всю область определения данной функции на три интервала
. Эти точки разбивают всю область определения данной функции на три интервала  ,
,  ,
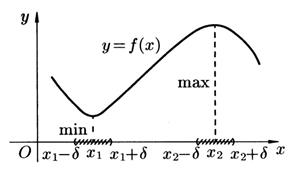
,  . Отметим на рисунке знаки производной слева и справа от каждой из критических точек.
. Отметим на рисунке знаки производной слева и справа от каждой из критических точек.


 – точка максимума,
– точка максимума,  , и
, и
 – точка минимума,
– точка минимума,  .
.
Иногда бывает удобным использовать другой достаточный признак существования экстремума, основанный на определении знака 2 –ой производной.
Теорема 8. Если в точке  первая производная функции
первая производная функции  равна нулю (
равна нулю ( ), а 2 –ая производная в точке
), а 2 –ая производная в точке 
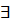 и отлична от нуля
и отлична от нуля
( ), то при
), то при  в точке
в точке  функция имеет максимум и минимум – при
функция имеет максимум и минимум – при  .
.

 непрерывна на отрезке
непрерывна на отрезке  , дифференцируема на интервале
, дифференцируема на интервале  и на концах отрезка принимает одинаковые значения
и на концах отрезка принимает одинаковые значения 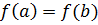 , то найдётся хотя бы одна точка
, то найдётся хотя бы одна точка  , в которой производная
, в которой производная  обращается в нуль, т.е.
обращается в нуль, т.е.  .
. и
и  . Если
. Если  , то функция
, то функция  в любой точке отрезка
в любой точке отрезка  , то функция достигает хотя бы одно из значений
, то функция достигает хотя бы одно из значений  интервала
интервала 
 найдётся точка, в которой касательная к графику параллельна оси
найдётся точка, в которой касательная к графику параллельна оси  . Может быть и не одна такая точка, например, две.
. Может быть и не одна такая точка, например, две. непрерывны на отрезке
непрерывны на отрезке  для
для  , то найдётся хотя бы одна точка
, то найдётся хотя бы одна точка  .
. , так как в противном случае по теореме Ролля нашлась бы точка
, так как в противном случае по теореме Ролля нашлась бы точка  , чего не может быть по условия теоремы.
, чего не может быть по условия теоремы.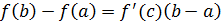 .
.
 для
для  .
.
 для
для  на возрастание и убывание.
на возрастание и убывание. .
. ;
; при
при  ;
;  при
при  .
. данная функция возрастает на интервалах
данная функция возрастает на интервалах 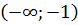 и
и  ; убывает на интервале
; убывает на интервале  .
. называется точкой максимума функции
называется точкой максимума функции 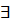 такая
такая  – окрестность точки
– окрестность точки 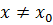 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство  .
.
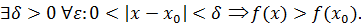
 .
. Геометрически равенство
Геометрически равенство Обратная теорема неверна, т.е. если
Обратная теорема неверна, т.е. если  её производная
её производная  равна нулю при
равна нулю при  , но
, но  Существуют функции, которые в точках экстремума не имеют производной. Например, непрерывная функция
Существуют функции, которые в точках экстремума не имеют производной. Например, непрерывная функция  в точке
в точке 
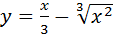 .
. . Находим
. Находим  , т.е.
, т.е.  .
. при
при  и равна нулю при
и равна нулю при  . Эти точки разбивают всю область определения данной функции на три интервала
. Эти точки разбивают всю область определения данной функции на три интервала  ,
,  ,
,  . Отметим на рисунке знаки производной слева и справа от каждой из критических точек.
. Отметим на рисунке знаки производной слева и справа от каждой из критических точек.
 , и
, и .
.
 ), то при
), то при  в точке
в точке  .
.


