Пусть функция  непрерывна на отрезке
непрерывна на отрезке  . Как известно, такая функция достигает своих наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точке
. Как известно, такая функция достигает своих наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точке  отрезка
отрезка  , либо на границе отрезка, т.е. при
, либо на границе отрезка, т.е. при  или
или  . Если
. Если  , то точку
, то точку  следует искать среди критических точек данной функции.
следует искать среди критических точек данной функции.
 Получаем следующее правило нахождения набольшего и наименьшего значений функции на
Получаем следующее правило нахождения набольшего и наименьшего значений функции на  :
:
1) найти критические точки функции на интервале  ;
;
2) вычислить значения функции в найденных точках;
3) вычислить значения функции на концах отрезка, т.е. в точках  и
и  ;
;
4) среди всех вычисленных значений функции выбрать наибольшее и наименьшее.
Замечания:
1. Если функция  на отрезке на отрезке  имеет лишь одну критическую точку и она является точкой максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение. На рисунке имеет лишь одну критическую точку и она является точкой максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение. На рисунке  (нб – наибольшее, – максимальное). (нб – наибольшее, – максимальное).
|
2. Если функция  на отрезке на отрезке  не имеет критических точек, то это означает, что на нём функция монотонно возрастает или убывает. не имеет критических точек, то это означает, что на нём функция монотонно возрастает или убывает.  своё наибольшее значение ( своё наибольшее значение ( ) функция принимает на одном конце отрезка, а наименьшее ( ) функция принимает на одном конце отрезка, а наименьшее ( ) – на другом. ) – на другом.
|
Пример. Найти наибольшее и наименьшее значение функции
 на отрезке
на отрезке 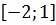 .
.
Находим критические точки данной функции:
 ;
;
 при
при 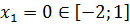 и при
и при  . Находим
. Находим  ,
,  ,
, 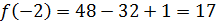 ,
,  . Итак,
. Итак,  в точке
в точке  ,
,  в точке
в точке  .
.

 непрерывна на отрезке
непрерывна на отрезке  . Как известно, такая функция достигает своих наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точке
. Как известно, такая функция достигает своих наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точке  отрезка
отрезка  или
или  . Если
. Если  , то точку
, то точку  Получаем следующее правило нахождения набольшего и наименьшего значений функции на
Получаем следующее правило нахождения набольшего и наименьшего значений функции на  ;
; и
и  ;
; (нб – наибольшее, – максимальное).
(нб – наибольшее, – максимальное).
 своё наибольшее значение (
своё наибольшее значение ( ) функция принимает на одном конце отрезка, а наименьшее (
) функция принимает на одном конце отрезка, а наименьшее ( ) – на другом.
) – на другом.
 на отрезке
на отрезке 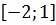 .
. ;
; при
при 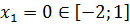 и при
и при  . Находим
. Находим  ,
,  ,
, 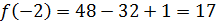 ,
,  . Итак,
. Итак,  в точке
в точке  ,
,  в точке
в точке  .
.


