Часть работы.СЛАУ.
[1] Постулат – утверждение принимаемое без доказательства, как аксиома. О справедливости того или иного постулата можно судить путем сравнения с экспериментом результатов, полученных при использовании того или иного постулата.
Оружие победы 2. Легкие танки
| БТ-2
| 



| | БТ-5
| 



| | БТ-7
| 



| | Танк
М3А1
Стюарт
(ленд-лиз)
| 



| | Танк
МКVII
Тетрарх
(ленд-лиз)
| 



| | Танк
МК III
Валентайн
(ленд-лиз)
| 



| | Танк
Т-26
| 



| | Танк
Т-50
| 



| | Танк
Т-60
| 



| | Т-70
| 



| | САУ
СУ-76
| 



|
Метод деления отрезка пополам.
Интервал изоляции [-7;-6].
| i
| a
| b
| c
| F(a)
| F(c)
| |b-a|
| |
| -7
| -6
| -6,5
|
| 10,75967
|
| |
| -6,5
| -6
| -6,25
| 10,759668
| 0,796755
| 0,5
| |
| -6,25
| -6
| -6,125
| 0,7967554
| -3,34813
| 0,25
| |
| -6,25
| -6,125
| -6,1875
| 0,7967554
| -1,34018
| 0,125
| |
| -6,25
| -6,1875
| -6,21875
| 0,7967554
| -0,28821
| 0,0625
| |
| -6,25
| -6,21875
| -6,23438
| 0,7967554
| 0,250101
| 0,03125
| |
| -6,23438
| -6,21875
| -6,22656
| 0,2501008
| -0,02009
| 0,015625
| |
| -6,23438
| -6,22656
| -6,23047
| 0,2501008
| 0,114745
| 0,007813
| |
| -6,23047
| -6,22656
| -6,22852
| 0,1147445
| 0,047261
| 0,003906
| |
| -6,22852
| -6,22656
| -6,22754
| 0,0472615
| 0,013569
| 0,001953
| |
| -6,22754
| -6,22656
| -6,22705
| 0,0135686
| -0,00327
| 0,000977
| c=(-7-6)/2=-6,5
f(a)=0,5-7-1-(-7-2)2-7=39
f(c)=0,5-6,5-1-(-6,5-2)2-6,5=10,75967
f(a)* f(c)>0
Интервал изоляции [1;2].
| i
| a
| b
| c
| F(a)
| F(c)
| |b-a|
| |
|
|
| 1,5
| -0,5
| 0,603553
|
| |
|
| 1,5
| 1,25
| -0,5
| 0,107948
| 0,5
| |
|
| 1,25
| 1,125
| -0,5
| -0,18212
| 0,25
| |
| 1,125
| 1,25
| 1,1875
| -0,182123
| -0,03359
| 0,125
| |
| 1,1875
| 1,25
| 1,21875
| -0,033593
| 0,038053
| 0,0625
| |
| 1,1875
| 1,21875
| 1,203125
| -0,033593
| 0,002449
| 0,03125
| |
| 1,1875
| 1,203125
| 1,195313
| -0,033593
| -0,01552
| 0,015625
| |
| 1,195313
| 1,203125
| 1,199219
| -0,015518
| -0,00652
| 0,007813
| |
| 1,199219
| 1,203125
| 1,201172
| -0,006521
| -0,00203
| 0,003906
| |
| 1,201172
| 1,203125
| 1,202148
| -0,002033
| 0,000209
| 0,001953
| |
| 1,201172
| 1,202148
| 1,20166
| -0,002033
| -0,00091
| 0,000977
| c=(1+2)/2=1,5
f(a)=0,51-1-(2-2)2+1=-0,5
f(c)=0,51,5-1-(1,5-2)2+1,5=0,603553
f(a)* f(c)<0
Интервал изоляции [3;4].
| i
| a
| b
| c
| F(a)
| F(c)
| |b-a|
| |
|
|
| 3,5
| 1,125
| 0,338388
|
| |
| 3,5
|
| 3,75
| 0,338388
| -0,23817
| 0,5
| |
| 3,5
| 3,75
| 3,625
| 0,338388
| 0,065427
| 0,25
| |
| 3,625
| 3,75
| 3,6875
| 0,065427
| -0,08254
| 0,125
| |
| 3,625
| 3,6875
| 3,65625
| 0,065427
| -0,0076
| 0,0625
| |
| 3,625
| 3,65625
| 3,640625
| 0,065427
| 0,029154
| 0,03125
| |
| 3,640625
| 3,65625
| 3,648438
| 0,029154
| 0,010838
| 0,015625
| |
| 3,648438
| 3,65625
| 3,652344
| 0,010838
| 0,001635
| 0,007813
| |
| 3,652344
| 3,65625
| 3,654297
| 0,001635
| -0,00298
| 0,003906
| |
| 3,652344
| 3,654297
| 3,65332
| 0,001635
| -0,00067
| 0,001953
| |
| 3,652344
| 3,65332
| 3,652832
| 0,001635
| 0,000482
| 0,000977
| c=(3+4)/2=3,5
f(a)=0,53-1-(3-2)2+3=1,125
f(c)=0,53,5-1-(3,5-2)2+3,5=0,338388
f(a)* f(c)>0
2. Метод Ньютона.
Условие начального приближения
f(x)*f''(x)>0
Интервал изоляции [-7;-6].
| k
| xi
| Xi+1 –Xi
| F(xi)
| f'(xi)
| |
| -7
| 0,559358
|
| -69,7228
| |
| -6,44064
| 0,193172
| 8,176259
| -42,3264
| |
| -6,24747
| 0,020124
| 0,7077
| -35,1676
| |
| -6,22735
| 0,000202
| 0,006952
| -34,4783
| |
| -6,22715
|
| 6,91E-07
| -34,4715
| | x
| f
| f''
| | -7
|
| 59,497986
| | -6
| -7
| 28,748993
|
f(-7)=0,5-7-1-(-7-2)2-7=39
f''(x)=0,5x *ln0.5-5*x+5;
f''(x)=0.5x*(ln0.5)2-5;
f'(-7)= 0,5-7 *ln0.5-5*(-7)+5 =-69.7228
f(-7)* f''(-7)= 39*59.497986>0
x1=x0- f(x)/ f'(x)=-7+39/(-69.7228)=-6.44064
|X1-X0|=-0,55936>0,001
Интервал изоляции [1;2].
| k
| xi
| Xi+1 –Xi
| F(xi)
| f'(xi)
| |
|
| 0,188436
| -0,5
| 2,653426
| |
| 1,188436
| 0,01355
| -0,03142
| 2,318991
| |
| 1,201986
| 7,16E-05
| -0,00016
| 2,294734
| |
| 1,202057
|
| -4,6E-09
| 2,294605
| | x
| f
| f''
| |
| -0,5
| -1,759773
| |
| 1,25
| -1,879887
|
f(1)=-0.5
f''(x)=0,5x *ln0.5-5*x+5;
f''(x)=0.5x*(ln0.5)2-5;
f'(1) =-1.759773
f(1)* f''(1)= -0.5*(-1.759773)>0
x1=x0- f(x)/ f'(x)=1+0.5/2.653426=1.188436
|X1-X0|>0,001
Интервал изоляции [3;4].
| k
| xi
| Xi+1 –Xi
| F(xi)
| f'(xi)
| |
|
| -0,30805
| -0,9375
| -3,04332
| |
| 3,691948
| -0,0383
| -0,09336
| -2,43753
| |
| 3,653646
| -0,00061
| -0,00144
| -2,36237
| |
| 3,653036
|
| -3,6E-07
| -2,36117
| | x
| f
| f''
| |
| 1,125
| -1,939943
| |
| -0,9375
| -1,969972
|
f(4)=-0.9375
f''(x)=0,5x *ln0.5-5*x+5;
f''(x)=0.5x*(ln0.5)2-5;
f'(4) =-3.04332
f(4)* f''(4)= -0.9375*(-1.939943)>0
x1=x0- f(x)/ f'(x)=4+0.9375/(-3.04332)=3.691948
|X1-X0|>0,001
Метод Чебышева.
xk+1 =xk – (f(xk))/f'(xk) - (f(xk)* f''(xk))/ 2(f'(xk))3 ;
Интервал изоляции [-7;-6].
| k
| xk
| Xk+1 –Xk
| F(xk)
| f'(xk)
| f''(xk)
| |
| -7
| 0,562781
|
| -69,7228
| 59,49799
| |
| -6,43722
| 0,192484
| 8,031607
| -42,1906
| 39,63389
| |
| -6,24474
| 0,017682
| 0,61162
| -35,0733
| 34,43372
| |
| -6,22705
| -9,4E-05
| -0,0032
| -34,4683
| 33,98989
| |
| -6,22715
|
| 4,59E-05
| -34,4715
| 33,99224
|
x 1 =-7 – (39)/(-69.7228) - 39* 59.49799/ 2(-69.7228) 3=-6.43722
Интервал изоляции [1;2].
| k
| xk
| Xk+1 –Xk
| F(xk)
| f'(xk)
| f''(xk)
| |
|
| 0,164886
| -0,5
| 2,653426
| -1,75977
| |
| 1,164886
| 0,030778
| -0,08653
| 2,361084
| -1,78572
| |
| 1,195665
| 0,005303
| -0,01471
| 2,306053
| -1,79024
| |
| 1,200968
| 0,000904
| -0,0025
| 2,296556
| -1,79101
| |
| 1,201872
|
| -0,00043
| 2,294937
| -1,79114
|
x 1 =1 – (-0.5)/(2,653426) – (-0.5)* (-1,75977)/ 2(2,653426) 3=1,164886
Интервал изоляции [3;4].
| k
| xk
| Xk+1 –Xk
| F(xk)
| f'(xk)
| f''(xk)
| |
|
| -0,27529
| -0,9375
| -3,04332
| -1,96997
| |
| 3,724709
| -0,05873
| -0,17427
| -2,50185
| -1,96366
| |
| 3,665978
| -0,01066
| -0,03072
| -2,38656
| -1,96215
| |
| 3,655322
| -0,00188
| -0,0054
| -2,36566
| -1,96187
| |
| 3,653439
|
| -0,00095
| -2,36196
| -1,96182
|
x 1 =4 – (-0,9375)/(-3,04332) -(-0,9375) * (-1.96997)/ 2(-3,04332) 3=3,724709
Сравнение результатов, полученных по разным методам решения[3;4].
| метод
| значение
| количество
| | решения
| корня
| итераций
| | деление отрезка пополам
| 3,652832
|
| | Метод Чебышева
| 3,653439
|
| | Ньютона
| 3,653036
|
|
Более выгоден метод Ньютона т.к. он потребовал меньшее количество итераций.
Часть работы.СЛАУ.
 Постановка задачи. Требуется найти решение системы m линейных уравнений, которая в общем виде записывается в виде Постановка задачи. Требуется найти решение системы m линейных уравнений, которая в общем виде записывается в виде
36х1-5x2-11х3 -19х4=-9
х1+33х2-11х3-20х4=-8
5х1-х2+26х3-19х4=-7
11х1+4х2-5х3+21х4=-6
В матричном виде эта система уравнений записывается так:
А х=f, где
  36 -5 -11 -19 36 -5 -11 -19
А = 1 33 -11 -20 - матрица системы,
5 -1 26 -19
11 4 -5 21
 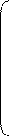 -9 х1 -9 х1
b= -8 - вектор правых частей х= х2 - вектор неизвестных
-7 х3
-6 х4
Таким образом, задача состоит в том, чтобы при известных коэффициентах матрицы А и элементах вектора f найти такие значения (х1,х2… хm) T, что при подстановке их в систему уравнений они превращаются в тождества.
Необходимым и достаточным условием существования единственного решения СЛАУ является условие det А ≠0. В случае равенства нулю определителя матрица называется вырожденной и при этом СЛАУ либо не имеет решения, либо имеет их бесчисленное множество.
Все методы решения линейных алгебраических задач можно разбить на два класса: прямые(методы Крамера, обратной матрицы и Гаусса) и итерационные(методы простой итерации, Якоби и Гаусса – Зейделя).
Метод обратной матрицы. Если det A ≠0, то существует матрица А-1, обратная к данной. Умножим исходную систему уравнений на обратную, получим: А-1А х= А-1 f.
Известно, что произведение обратной матрицы на исходную дает единичную матрицу Е, следовательно, получаем Е х= А- 1f, х= А -1f
Решение СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Т.о., задача решения СЛАУ и задача нахождения обратной матрицы связаны между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы.
Метод простой итерации. Преобразуем исходную систему линейных уравнений А х=f к эквивалентной системе вида:
х=хα+β, где
х – искомый вектор, а α и β – некоторые новые матрица и вектор соответственно. В качестве первого приближения можно взять хi(0)=0. Следующие приближения находим по рекуррентным формулам
х(к+1)= α;х(к)+β, к=0,1,2,…
Такой итерационный процесс будем называть методом простых итераций(МПИ). Достаточным условием сходимости МПИ к решению системы при любом начальном векторе х(0) является требование || α;||<1, где || α;|| 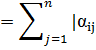 | - норма матрицы α;. | - норма матрицы α;.
Существует несколько способов построения порождающей матрицы α;, для которой выполняется достаточное условие сходимости.
Метод Гаусса- Зейделя
В отличии от метода Якоби, в котором вычисление всех компонент вектора (k+1)-го приближения проводилось однообразно, в методе Гаусса- Зейделя для расчета i-й компоненты следующего приближения используется уже вычисленное на том, т.е. (k+1)-м шаге, новые значения первых i-1 компонент:
X1(k+1)=1/a11(f1-a11(k)-a13x3(k)-…-a1mxm(k))
X2(k+1)=1/a22(f2-a21(k+1)-a23x3(k)-…-a2mxm(k))
Xi(k+1)=1/aij(fi-ai1(k+1)-ai2x2(k+1)-…-ai,i-1xi-1(k+1)- ai,i+1xi+1(k)-…-a2mxm(k))
Xm(k+1)=1/amm(fm-am1(k+1)-am2x2(k+1)-…-am,m-1xm-1(k+1))
Или, в компактном виде:
Xi(k+1)=1/aij(fi-  xj(k+1)- xj(k+1)- 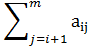 xj(k)), i=1,2…,m. xj(k)), i=1,2…,m.
Достаточным условием сходимости этого метода, как и для метода Якоби, является условие диагонального преобладания:
/ aij/> 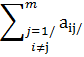 , i=1,2…,m. , i=1,2…,m.

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|
Краткая психологическая характеристика возрастных периодов.Первый критический период развития ребенка — период новорожденности Психоаналитики говорят, что это первая травма, которую переживает ребенок, и она настолько сильна, что вся последующая жизнь проходит под знаком этой травмы...
РЕВМАТИЧЕСКИЕ БОЛЕЗНИ Ревматические болезни(или диффузные болезни соединительно ткани(ДБСТ))— это группа заболеваний, характеризующихся первичным системным поражением соединительной ткани в связи с нарушением иммунного гомеостаза...
Решение Постоянные издержки (FC) не зависят от изменения объёма производства, существуют постоянно...
|
Концептуальные модели труда учителя В отечественной литературе существует несколько подходов к пониманию профессиональной деятельности учителя, которые, дополняя друг друга, расширяют психологическое представление об эффективности профессионального труда учителя...
Конституционно-правовые нормы, их особенности и виды Характеристика отрасли права немыслима без уяснения особенностей составляющих ее норм...
Толкование Конституции Российской Федерации: виды, способы, юридическое значение Толкование права – это специальный вид юридической деятельности по раскрытию смыслового содержания правовых норм, необходимый в процессе как законотворчества, так и реализации права...
|
|













































 Постановка задачи. Требуется найти решение системы m линейных уравнений, которая в общем виде записывается в виде
Постановка задачи. Требуется найти решение системы m линейных уравнений, которая в общем виде записывается в виде
 36 -5 -11 -19
36 -5 -11 -19

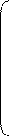 -9 х1
-9 х1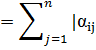 | - норма матрицы α;.
| - норма матрицы α;. xj(k+1)-
xj(k+1)- 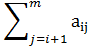 xj(k)), i=1,2…,m.
xj(k)), i=1,2…,m.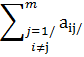 , i=1,2…,m.
, i=1,2…,m.


