УРОВНИ ИЗМЕРЕНИЯ
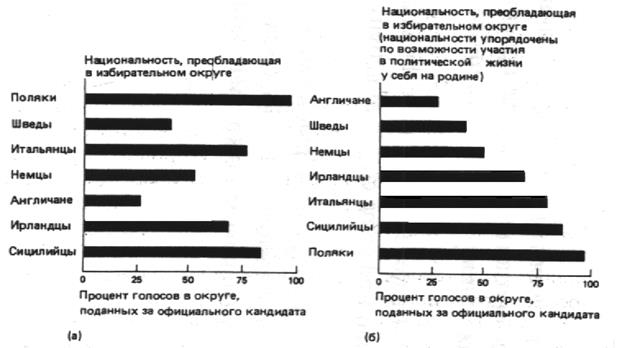
Процедуры измерения предоставляют средство категоризации и упорядочения явлений. Вместе с тем одни процедуры дают возможность выявить более тонкие и детальные различия между событиями, чем другие. Поэтому нам приходится констатировать различные уровни измерения. Говоря о том, что процедура обеспечивает данный уровень измерения, мы квалифицируем ее в соответствии с количеством поставляемой ею информации об измеряемых явлениях и их взаимоотношениях друг с другом. Уровни измерения носят название номинального, порядкового и интервального. Номинальное измерение представляет минимальную информацию о явлении. Оно дает лишь набор дискретных категорий, позволяющих разграничить разные объекты. Номинальное измерение – это простое наименование объектов в соответствии с заранее заданной схемой классификации. Национальность обычно “измеряется” на номинальном уровне посредством классификации людей на англичан, швейцарцев, бразильцев и т. п. Это “измерение” не сообщает, насколько характеристика “национальность” свойственна разным людям, и не позволяет упорядочивать их. Использование номинального измерения всего лишь дает возможность объединить объекты в классы, обозначенные так, как это принято в классификационной схеме. Чтобы быть полезными, схемы номинального измерения должны основываться на множествах категорий, которые являются взаимоисключающими и исчерпывающими. Это означает, что (1) невозможно отнести один объект к более чем одной категории и (2) категории должны быть такими, чтобы каждый объект мог быть отнесен к той или иной категории. Если мы хотим расклассифицировать всех избирателей Соединенных Штатов с помощью схемы номинального измерения, мы не можем воспользоваться категориями демократ, республиканец, либерал и консерватор, так как они не являются взаимоисключающими. Поскольку американские политические партии обращаются к самым широким массам избирателей, человек вполне может оказаться одновременно демократом и консерватором или либералом, одновременно республиканцем и консерватором или либералом. Эти [c.82] категории не дают возможности провести разграничение между избирателями во всех случаях. Аналогично, если мы попытаемся расклассифицировать избирателей на основании партийной принадлежности, используя только две категории: республиканец и демократ, – мы обнаружим, что наши категории не являются исчерпывающими, так как некоторые избиратели считают себя независимыми либо членами других партий. Для упрощения анализа мы, быть может, захотим заменить категории в схеме номинального измерения числами. Важно понимать, однако, что в данном контексте эти числа не имеют реального значения – они всего лишь символы. Исходя из того, что мы решили заменить категорию республиканец цифрой 5, а категорию демократ – цифрой 1, мы не можем считать, что у республиканцев в пять раз больше приверженцев, чем у демократов. Любая категория номинального измерения может быть заменена любым числом, при условии, что у каждой категории будет свой индивидуальный номер. Порядковое измерение предоставляет больше информации, так как дает возможность не только категоризовать, но и упорядочивать, или ранжировать, явления. Порядковое измерение позволяет присваивать каждому объекту число, которое обозначает не только то, что данный объект отличен от одних объектов и сходен с другими с точки зрения измеряемой переменной, это число указывает также, как именно данный объект связан с другими в терминах количества того конкретного свойства, которым он характеризуется. Располагая порядковым измерением, мы можем сказать, какие объекты характеризуются большим (или меньшим) количеством измеряемого свойства по сравнению с какими-то другими объектами; мы можем также расположить объекты по порядку в зависимости от количества того свойства, которое их характеризует. Такое упорядочение дает более детальную и более точную информацию, чем номинальное измерение. Понятие социальный класс обычно измеряется на порядковом уровне: каждому человеку приписывается ранг низшего, среднего или высшего класса. Интервальное измерение предоставляет еще больше информации. Мы можем не только классифицировать и упорядочивать объекты, после того как они измерены на [c.83] интервальном уровне, но и сказать, насколько большим или меньшим количеством измеряемого свойства по сравнению с другими объектами они характеризуются. Порядковое измерение не основано ни на какой стандартной для данной переменной единице и не позволяет установить, насколько далеко в терминах этой переменной отстоят друг от друга разные объекты. Оно лишь позволяет говорить, что у одних объектов данная переменная имеет большее или меньшее значение, чем у других. Интервальное измерение основано на представлении о существовании некоторой стандартной единицы измеряемого свойства. В то время как порядковые измерения дают нам лишь огрубленное представление об отношении между объектами с точки зрения данной переменной, интервальные измерения предоставляют информацию о “расстоянии” между ними. Хороший пример такого рода – переменная доход. Доход обычно измеряется в денежных единицах (в Соединенных Штатах это доллары и центы). Поскольку при измерении используются стандартные единицы, мы можем утверждать, что между 10000 и 11000 долларов годового дохода разница абсолютно та же, что и между 50000 и 51000 долларов. Мы не в состоянии сделать этого с помощью порядкового измерения. Если измерять доход с помощью порядкового измерения, разделяя людей по их доходу на такие категории, как доход ниже 5000 долларов и доход от 5000 до 9999 долларов, мы сможем сказать, что у одного человека доход выше или ниже, чем у другого, однако мы не сможем сказать точно, насколько эти люди различаются по своим доходам, так как не знаем, где именно находится человек внутри своей категории. Различие в доходе между человеком из категории 1 (до 5000 долларов) и человеком из категории 2 (от 5000 до 9999 долларов) может составлять всего лишь один доллар (5 000 долларов минус 4 999 долларов), а может доходить до 9999 долларов (9999 долларов минус 0 долларов) в зависимости от точной цифры их доходов, однако мы не можем увидать этой разницы, исходя из порядкового измерения. Помимо того что интервальное измерение дает нам точную информацию об абсолютных различиях между объектами, мы также получаем возможность делать [c.84] точные утверждения об относительных различиях между понятиями. Мы, например, можем согласиться с тем, что население 50000 человек – это в два раза больше, чем население 25000 человек, потому что ведь есть такие места, где вообще никто не живет: в истинных интервальных измерениях существует нулевая точка, и по крайней мере теоретически возможно существование объектов, имеющих на таких шкалах нулевую отметку. Так как на порядковой шкале не существует осмысленной нулевой точки, мы не можем говорить, например, что люди высшего класса имеют в два раза большее количество “класса”, чем люди низшего класса, – мы не знаем, что означает “не иметь никакого классового статуса”. На основании всего этого следует сделать одно важное замечание относительно уровня измерения. Когда речь идет о сравнении явлений, измерения номинального уровня – наименее полезный тип измерения. Если мы используем его в ситуации, когда возможно использовать “более высокий” (более точный) уровень измерения, мы можем потерять потенциально ценную информацию. Если при изучении поведения на выборах мы приводим классификацию людей на республиканцев, независимых и демократов, в то время как можно задать другой набор вопросов и осуществить их ранговое упорядочение с учетом [c.85] перехода от более сильной к более слабой партийной идентификации, мы, возможно, отказываемся от информации, которая поможет нам понять наблюдаемые отношения. Измерение порядкового уровня полезнее, чем измерение номинального уровня, но у него также есть свои ограничения. Интервальное измерение – наиболее желательная форма измерения как в силу того, что оно дает наиболее детальную информацию, так и потому, что оно позволяет осуществлять математическую обработку имеющихся данных. (Подробнее об этом будет говориться в гл. 14,15 и 16.) Наша задача состоит в том, чтобы там, где это возможно и удобно, стремиться к операционализациям, позволяющим осуществлять измерение интервального уровня. Однако каким образом мы выбираем уровень измерения, подходящий для конкретных понятий, операционализацией которых мы занимаемся? Это проблема как концептуализации, так и технологии измерения. В процессе исследования на этапе построения теории мы должны прежде всего спросить себя, лежит ли в основе различий, наблюдаемых в отдельных случаях, некий континуум. Если да, то мы можем предложить для данного понятия порядковое или даже интервальное измерение, в противном случае в качестве измерения может выступать лишь номинальная классификация. Поясним важность этого на примере. Предположим, мы изучаем зависимость между национальностью иммигрантов и степенью поддержки ими политического механизма большого города США начала XX века. Если мы осуществляем операционализацию национальности на номинальном уровне и категоризуем поддержку политического механизма в городских избирательных округах, мы, возможно, получим картину, подобную той, что изображена на рис.3.2а.
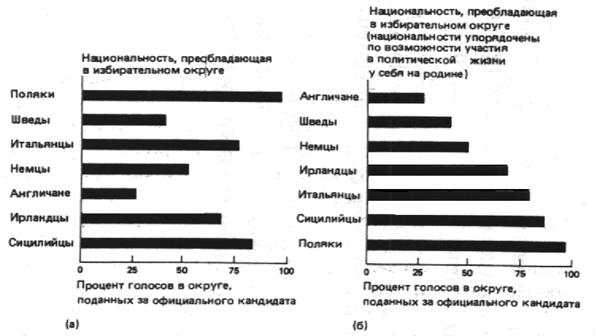
Рис. 3.2. Пример воздействия уровня измерения на интерпретацию данных Здесь не видно никакой отчетливой связи между национальностью и поведением на выборах, так как знание о том, какая национальность преобладает в данном округе, не позволяет ранжировать его относительно других округов. Однако если мы проанализируем ход наших рассуждений, то сможем понять, что наши ожидания относительно связи национальности с поддержкой политического механизма имеют определенные основания: соответствующие страны [c.86] происхождения различны с точки зрения возможности участия в политической жизни, которое они предоставляют своим гражданам. Мы можем сделать вывод, что те, кто имеет небольшой опыт существования в условиях демократии, будут с готовностью передавать свое право на самоуправление политическим лидерам. Если исходить из этого и упорядочить страны в соответствии допускаемой ими степенью участия своих граждан в политике, мы можем построить график, подобный тому, что изображен на рис.3.2б. На этом графике отчетливо видна взаимосвязь национальности с поддержкой политического механизма. Упорядочение категорий по независимой переменной помогает выявить систему в ее отношениях с зависимой переменной.
Рис. 3.2. Пример воздействия уровня измерения на интерпретацию данных Если у нас хватит смелости, мы можем даже повысить уровень измерения независимой переменной до интервального. Мы, например, могли бы подсчитать количество постановлений, касающихся участия в политической жизни, в законодательствах соответствующих стран на протяжении нескольких лет, непосредственно предшествующих началу широкой иммиграции в США. Полученные цифры можно использовать для ранжирования национальностей на интервальной шкале и осуществить даже более точное сравнение независимой и зависимой переменных. Сможем ли мы осуществить такое повышение ранга переменных, чтобы перейти от номинального уровня измерения к порядковому или интервальному, зависит как от разработки теоретического обоснования такого перехода, так и от наличия технических возможностей применения операционных процедур, осуществляющих измерения более высокого уровня. Даже если мы сможем в нашем примере выразить понятие национальности в терминах интервального уровня, мы, возможно, не получим в свое распоряжение законодательные акты, необходимые для расположения стран на интервальной шкале. В этом случае наши возможности по получению измерений более высокого уровня ограничивает измерительная техника. Примеры такого рода достаточно многочисленны. Например, при исследовании взаимосвязи между полом и политическим поведением у нас будет возможность утверждать, что мужские черты характера – это свойство, [c.87] которым люди обладают в разной степени (те, кто обладает им в наименьшей степени, – женщины). Если мы можем выступить с набором вопросов для выяснения того, насколько люди обладают этим свойством (если вообще обладают), мы в принципе можем упорядочить людей на порядковой или интервальной шкале “мужественности”. Однако если мы не располагаем денежными средствами для проведения исследования, в ходе которого люди ответят на эти вопросы, нам придется рассчитывать на номинальную классификацию мужчина/женщина, сведения о которой мы находим в списках членов партии. Эти ситуационные факты затрудняют установление правил того, как операционализировать понятия с целью достичь определенных уровней измерения. Однако мы полагаем, что можно следовать правилу операционализации У.Ф.Шайвли 3. Он советует использовать максимально точные для данного объекта измерения и не терять информацию за счет неточного измерения. Это обычно означает применение более строгих процедур измерения, которые там, где это возможно, осуществляли бы измерение более высоких уровней. Не довольствуйтесь операционализацией, дающей номинальное измерение, когда теоретически оправданно и технически возможно порядковое или интервальное измерение. Сделав данные замечания, мы должны сказать о некоторых исключениях из основного правила. Существуют случаи, когда слишком большая точность измерения на самом деле нежелательна. Один пример такого рода приводит Шайвли. Из его работы заимствован (с некоторыми изменениями) рис.3.3. На рисунке двумя разными способами изображена зависимость между возрастом и голосованием на президентских выборах 1968 г. На рис.3.3а возраст измеряется в годах. Поскольку в каждой возрастной группе (например, 21–22 года, 35–36 лет, 50– 51 год) оказывается немного людей, на диаграмме не выявляется никакой отчетливой структуры отношений между двумя переменными. На рис.3.3б возраст измеряется менее точно – в пятилетиях. Наличие в каждой группе большого числа объектов позволяет увидеть явную структуру отношений: вероятность голосования повышается до 50-летнего возраста, а затем, вообще говоря, снижается. [c.88]
Рис. 3.3. Пример воздействия на интерпретацию группировки данных (взят из кн.: Shively W.Ph. The Craft of Political Research, 2nd ed. – Englewood Cliffs (N.J.): Prentice-Hall, 1980, p. 67-68). [c.89] Пожертвовав некоторой точностью измерения, мы получили выигрыш с точки зрения простоты анализа. Это удачная сделка, пока мы не зашли столь далеко по пути уменьшения точности, чтобы вновь потерять из виду изучаемые соотношения. Если мы используем для измерения возраста 20-летний интервал, мы не увидим больших количественных различий между возрастными группами голосующих и сможем прийти к выводу, что возраст не связан с вероятностью голосования. Поскольку заранее до реального анализа данных мы, как правило, не знаем, какая точность окажется необходимой для выявления соотношений, мы должны следовать правилу, в соответствии с которым осуществляется по возможности максимально точная операционализация понятий. Мы всегда сумеем отказаться от ненужной точности путем “сжатия категорий” (перехода к более крупным различительным единицам), если сочтем это нужным. Однако если не собрать информацию в самом начале, мы не сможем обратиться к ней в дальнейшем. [c.90]
|