Матрица парных коэффициентов корреляции
Анализ межфакторных (между «иксами»!) коэффициентов корреляции показывает, что значение 0,8 превышает по абсолютной величине только коэффициент корреляции между парой факторов Х 1– Х 3 (выделен жирным шрифтом). Факторы Х 1– Х 3, таким образом, признаются коллинеарными.
2. Как было показано в пункте 1, факторы Х 1– Х 3 являются коллинеарными, а это означает, что они фактически дублируют друг друга, и их одновременное включение в модель приведет к неправильной интерпретации соответствующих коэффициентов регрессии. Видно, что фактор Х 3 имеет больший по модулю коэффициент корреляции с результатом Y, чем фактор Х 1: ry , x 1=0,519; ry , x 3=0,610; Для построения уравнения регрессии значения используемых переменных (Y, X 2, X 3, X 4, X 5, X 6) скопируем на чистый рабочий лист (прил. 3). Уравнение регрессии строим с помощью надстройки «Анализ данных… Регрессия» (меню «Сервис» ® «Анализ данных…» ® «Регрессия»). Панель регрессионного анализа с заполненными полями изображена на рис. 2. Результаты регрессионного анализа приведены в прил. 4 и перенесены в табл. 2. Уравнение регрессии имеет вид (см. «Коэффициенты» в табл. 2):
Уравнение регрессии признается статистически значимым, так как вероятность его случайного формирования в том виде, в котором оно получено, составляет 8,80×10-6 (см. «Значимость F» в табл. 2), что существенно ниже принятого уровня значимости a=0,05. Вероятность случайного формирования коэффициентов при факторах Х 3, Х 4, Х 6 ниже принятого уровня значимости a=0,05 (см. «P-Значение» в табл. 2), что свидетельствует о статистической значимости коэффициентов и существенном влиянии этих факторов на изменение годовой прибыли Y. Вероятность случайного формирования коэффициентов при факторах Х 2 и Х 5 превышает принятый уровень значимости a=0,05 (см. «P-Значение» в табл. 2), и эти коэффициенты не признаются статистически значимыми.
рис. 2. Панель регрессионного анализа модели Y (X 2, X 3, X 4, X 5, X 6)
Таблица 2 Результаты регрессионного анализа модели Y (X 2, X 3, X 4, X 5, X 6)
3. По результатам проверки статистической значимости коэффициентов уравнения регрессии, проведенной в предыдущем пункте, строим новую регрессионную модель, содержащую только информативные факторы, к которым относятся: · факторы, коэффициенты при которых статистически значимы; · факторы, у коэффициентов которых t ‑статистика превышает по модулю единицу (другими словами, абсолютная величина коэффициента больше его стандартной ошибки). К первой группе относятся факторы Х 3, Х 4, Х 6, ко второй — фактор X 2. Фактор X 5 исключается из рассмотрения как неинформативный, и окончательно регрессионная модель будет содержать факторы X 2, X 3, X 4, X 6. Для построения уравнения регрессии скопируем на чистый рабочий лист значения используемых переменных (прил. 5) и проведем регрессионный анализ (рис. 3). Его результаты приведены в прил. 6 и перенесены в табл. 3. Уравнение регрессии имеет вид:
(см. «Коэффициенты» в табл. 3).
рис. 3. Панель регрессионного анализа модели Y (X 2, X 3, X 4, X 6)
Таблица 3 Результаты регрессионного анализа модели Y (X 2, X 3, X 4, X 6)
Уравнение регрессии статистически значимо: вероятность его случайного формирования ниже допустимого уровня значимости a=0,05 (см. «Значимость F» в табл. 3). Статистически значимыми признаются и коэффициенты при факторах Х 3, Х 4, Х 6: вероятность их случайного формирования ниже допустимого уровня значимости a=0,05 (см. «P-Значение» в табл. 3). Это свидетельствует о существенном влиянии годового размера страховых сборов X 3, годового размера страховых выплат X 4 и формы собственности X 6 на изменение годовой прибыли Y. Коэффициент при факторе Х 2 (годовой размер страховых резервов) не является статистически значимым. Однако этот фактор все же можно считать информативным, так как t ‑статистика его коэффициента превышает по модулю единицу, хотя к дальнейшим выводам относительно фактора Х 2 следует относиться с некоторой долей осторожности.
4. Оценим качество и точность последнего уравнения регрессии, используя некоторые статистические характеристики, полученные в ходе регрессионного анализа (см. «Регрессионную статистику» в табл. 3): · множественный коэффициент детерминации
показывает, что регрессионная модель объясняет 75,1 % вариации годовой прибыли Y, причем эта вариация обусловлена изменением включенных в модель регрессии факторов X 2, X 3, X 4 и X 6; · стандартная ошибка регрессии
показывает, что предсказанные уравнением регрессии значения годовой прибыли Y отличаются от фактических значений в среднем на 237,6 тыс. руб. Средняя относительная ошибка аппроксимации определяется по приближенной формуле:
где Е отн показывает, что предсказанные уравнением регрессии значения годовой прибыли Y отличаются от фактических значений в среднем на 26,7 %. Модель имеет неудовлетворительную точность (при
5. Для экономической интерпретации коэффициентов уравнения регрессии сведем в таблицу средние значения и стандартные отклонения переменных в исходных данных (табл. 4 ). Средние значения были определены с помощью встроенной функции «СРЗНАЧ», стандартные отклонения — с помощью встроенной функции «СТАНДОТКЛОН» (см. прил. 1).
Таблица 4
|

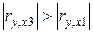 (см. табл. 1). Это свидетельствует о более сильном влиянии фактора Х 3 на изменение Y. Фактор Х 1, таким образом, исключается из рассмотрения.
(см. табл. 1). Это свидетельствует о более сильном влиянии фактора Х 3 на изменение Y. Фактор Х 1, таким образом, исключается из рассмотрения. .
.



 тыс. руб.
тыс. руб. %,
%,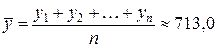 тыс. руб. — среднее значение годовой прибыли (определено с помощью встроенной функции «СРЗНАЧ»; прил. 1).
тыс. руб. — среднее значение годовой прибыли (определено с помощью встроенной функции «СРЗНАЧ»; прил. 1). — точность модели высокая, при
— точность модели высокая, при  — хорошая, при
— хорошая, при  — удовлетворительная, при
— удовлетворительная, при  — неудовлетворительная).
— неудовлетворительная).


