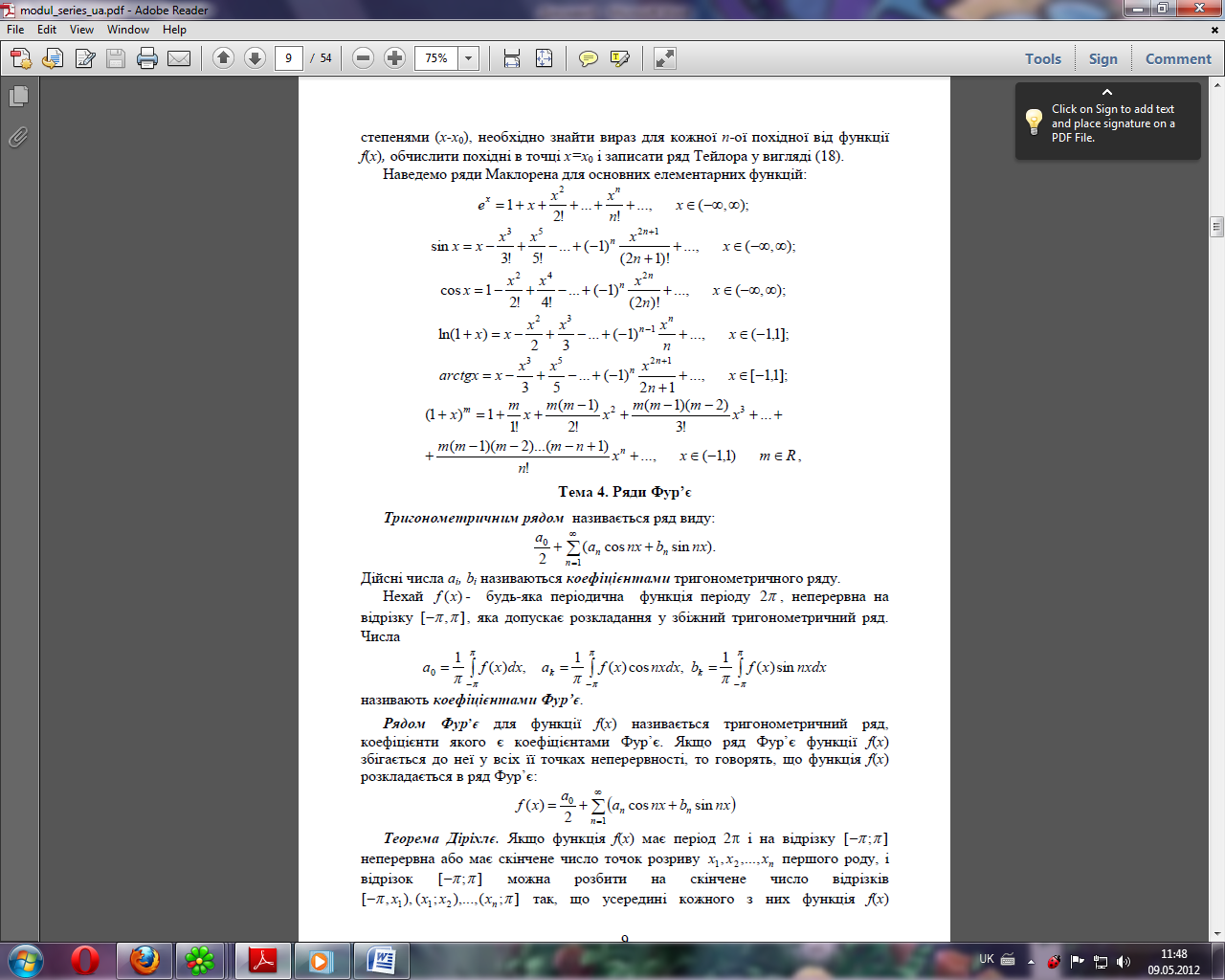
ЛОГИЧЕСКИЕ БЛОКИ ДЬЕНЕША

Для детей и взрослых!

Мы приглашаем Вас на уютный зимний праздник в наш лесной домик.

За время праздника мы:

- поиграем в подвижные зимние игры, покатаемся с горки;

- встретим в лесу Деда Мороза и загадаем новогодние желания;

- согреемся теплым чаем и пирогом у затопленного камина;

- откроем книгу сказок и прочтем удивительную новогоднюю историю;

Подарите себе и своим детям атмосферу тепла, уюта и волшебства наступающего Нового Года!

*Возможна доставка с пл. Южной (или с места по договоренности);

*Цена участия в программе 400 р. + цена за транспорт;

тел. 8-952-153-5029 предварительная запись ОБЯЗАТЕЛЬНА!

 

 

ЛОГИЧЕСКИЕ БЛОКИ ДЬЕНЕША

Золтан Дьенеш, изобретатель логических блоков – венгерский математик и педагог, развивший теорию «новой математики» и считавший, что учиться лучше не за партой, а играя. Играя, дети способны постигать очень сложные математические и логические концепции – вплоть до работы с абстрактными системами и символами.

Дьенеш считал, что умение работать с символами, понимать их язык – одна из последних, самых «сложных» стадий в развитии математического мышления.

Логические блоки – это развивающая игра, рассчитанная на детей от 2 до 10 лет.

Основная цель и задача - помочь детям научиться выполнять логические операции (то есть познакомиться с основой, сердцевиной математики) – разбивать объекты по свойствам, кодировать информацию, обобщать и находить различия, сравнивать, классифицировать объекты и т. д.

Блоки Дьенеша помогают детям:

Ø познакомиться с признаками объектов (формой, цветом, размером и т. д.)

Ø развить пространственное воображение, творческие способности, фантазию, навыки конструирования, моделирования, речь, логическое мышление, а также самостоятельность и произвольность

На каждом возрастном этапе - свой уровень «вхождения» в математику. И прелесть блоков венгерского математика именно в том, что с помощью них можно придумывать игры и занятия для каждого из возрастов – в соответствии с той информацией, которую ребенок готов усвоить.

Логические блоки – это «игра на вырост», которая будет полезной долгие годы. Логические блоки Дьенеша представляют собой игры, составленные на основе комплекта, который состоит из 48 геометрических фигур:

Ø четырех форм - круги, треугольники, квадраты, прямоугольники;

Ø трех цветов - красные, синие и желтые;

Ø двух размеров - большие, маленькие;

Ø двух объемов - толстые, тонкие.

В наборе нет ни одной одинаковой фигуры. Каждая геометрическая фигура характеризуется четырьмя признаками: формой, цветом, размером, толщиной. Вторая составляющая игры – карточки, на которых закодирована информация о геометрической фигуре и ее признаках. Одни кодовые карточки разделена на две части: первая указывает на то, какую геометрическую фигуру (логический блок) мы ищем; вторая содержит информацию о том, какого цвета эта фигура. На следующих карточках к указанной информации добавляются такие понятия, как величина геометрической фигуры и ее толщина.

В пособии Е.А. Носовой и Р.Л. Непомнящей «Логика и математика для дошкольников» представлены 4 группы постепенно усложняющихся игр и упражнений с логическими блоками:

I. для развития умений выявлять и абстрагировать свойства

II. для развития умений сравнивать предметы по их свойствам

III. для развития действий классификации и обобщения

Каждая группа представлена вариантами игр на развитие умения оперировать 1, 2 или 3(4) свойствами.