Контрольное задание №6
1. Между какими парами высказываний, приведенных ниже, существует отношение следствия? S1: Если прямая перпендикулярна радиусу окружности и проходит через точку пересечения радиуса с окружностью, то она – касательная к окружности. S2: Прямая есть касательная к окружности тогда и только тогда, когда она перпендикулярна к радиусу окружности и проходит через точку пересечения радиуса с окружностью. S3: Если прямая перпендикулярна к радиусу окружности, но не проходит через точку пересечения радиуса с окружностью, то она не является касательной к окружности.
2. Заданы следующие высказывания: S1: Если две прямые совпадают или не имеют общих точек, то они параллельны. S2: Две прямые параллельны тогда и только тогда, когда они совпадают или не имеют общих точек. S3: Если две прямые не совпадают и не имеют общих точек, то они параллельны. Между какими парами высказываний существует отношение следствия? Приведенные высказывания расположить таким образом, чтобы из каждого высказывания следовали все, стоящие после него.
3. Заданы следующие высказывания: если матч состоится, то Пётр и Сергей придут на него; Сергей или Пётр придут на матч в том и только в том случае, если он состоится; если матч не состоится, то ни Пётр ни Сергей не придут на него. Между какими парами высказываний существует отношение следствия?
4. Расположите следующие 5 высказываний в таком порядке, чтобы из каждого высказывания следовали все, стоящие после него:
5.Имеем высказывание: «Для того чтобы матрица имела обратную матрицу, необходимо и достаточно, чтобы её определитель был отличен от нуля». Какие из приведенных ниже высказываний следуют из данного? 1) Для того чтобы матрица имела обратную, достаточно, чтобы ее определитель был равен нулю. 2) Для того чтобы определитель матрицы был отличен от нуля, достаточно, чтобы эта матрица имела обратную. 3) Для того чтобы определитель матрицы был равен нулю, необходимо, чтобы эта матрица не имела обратной. 4) Матрица имеет обратную тогда и только тогда, когда её определитель равен нулю. 5) Определитель матрицы равен нулю только тогда, когда эта матрица не имеет обратной. Есть ли среди приведенных высказываний эквивалентные?
6. Какие из приведенных ниже высказываний являются эквивалентными? 1) Сидоров сдаст экзамен, если будет посещать лекции и заниматься самостоятельно. 2) Если Сидоров будет заниматься самостоятельно, но не посещать лекции, вряд ли он сдаст экзамен. 3) Сидоров сдаст экзамен только тогда, когда будет посещать лекции и заниматься самостоятельно. 4) Сидоров не сдаст экзамен, если не будет заниматься самостоятельно, даже если он будет посещать лекции. 5) Если Сидоров не сдаст экзамен, значит он не занимался самостоятельно или не посещал лекции. 6) Если Сидоров сдал экзамен, то он посещал лекции и занимался самостоятельно.
7. Какие из приведенных ниже высказываний эквивалентны? 1) Я решу эту задачу, только если пойму ее условие и хорошо буду знать теоретический материал. 2) Если я не смог решить задачу, значит я не знал теоретический материал или не понял условие задачи. 3) Если я хорошо знаю теоретический материал, но не понял условие задачи, решить задачу я не смогу. 4) Если не знаю теоретический материал или не понял условие задачи, то не смогу решить ее.
8. Как определить отношение следствия или эквивалентности между высказываниями с помощью диаграмм Эйлера-Венна?
9. С помощью диаграмм Эйлера-Венна определить, для каких пар высказываний, приведенных далее, имеет место отношение следствия или эквивалентности. S1: Иван и Петр правильно ответили на вопросы. S2: Если Иван правильно ответил на вопросы, то Петр – неверно. S3: Или Петр, или Иван неверно ответил на вопросы. S4: Или Иван неверно ответил на вопросы, или Петр правильно. S5: Иван верно ответил на вопросы, но Петр ошибся.
10. Пользуясь диаграммой Эйлера-Венна, определить, какие из приведенных пар высказываний, являются такими, что одно из них следует из другого. 1) 2) 3) 4)
|

 ;
;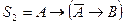 ;
; ;
; ;
; .
.






