Статья 1. Сфера применения настоящей Конвенции
І. Функція двох змінних. Функція
Розв’язавши рівняння (17) відносно
Це так звана формула диференціювання неявної функції. Нею подаються відносні швидкості зміни значень х щодо значень у, чим забезпечується незмінність f (x, y). Геометрично це означає, що точка (x, y) рухається вздовж кривої, рівняння якої є и = f (x, y), а (18) визначає для будь-якого моменту напрям її руху.
●Нехай
З рівняння (18) знаходимо:
●Нехай
знаходимо частинні похідні цієї функції за х і за у:
Підставляючи в (18), маємо:
За умовою х = 3, у = 1,
1. ● 2. ● 3. ● 4. ● 5. ●
ІІ. Функція трьох змінних. Нехай Р (х, у, z) — точка на поверхні, заданій рівнянням:
і нехай РС і АР — перерізи, що утворюються площинами, проведеними через точку Р паралельно площинам Y 0 Z і X 0 Z (рис. 1.24). Для точок кривої АР змінна у лишається сталою. Отже, згідно з (19) z є неявною функцією лише х, а на підставі (16) виконується рівність:
Геометрична інтерпретація. Формула (20) визначає тангенс кута нахилу кривої АР у точці Р до осі0 х.
Рис. 1.24 У лівій її частині замість Аналогічно нахил кривої РС до осі 0 y у точці Р задається рівнянням:
Знайти в точці (1, 1) частинні похідні функції u = f (x, y), заданої неявно:
●Маємо F (x, y, u) =
Функція F (x, y, u) дорівнює 0 в точці (1, 1, 5) і неперервна в її околі, а частинні похідні цієї функції
також неперервні. Отже, частинні похідні неявної функції можна знайти за формулами (20) і (21). Частинні похідні функції Тоді частинні похідні функції u = f (x, y) у цій точці такі: 1.2.10. Формула Тейлора для функції Нехай функція двох змінних z = f (x, y) в околі точки (x 0, y 0) має неперервні похідні всіх порядків до m включно. Тоді в цьому околі справджується рівність:
де Означення. Многочлен
називають многочленом Тейлора m -го порядку функції f (x, y),
— залишковим членом m -го порядку формули Тейлора. Формулу (23) називають формулою Тейлора m -го порядку функції f (x, y) в околі точки (x 0, y 0) із залишковим членом у формулі Пеано. Зокрема, при x 0 = y 0 = 0 формулу (23) називають формулою Маклорена. Якщо функція f (x, y) має в околі точки (x 0, y 0) неперервні похідні до (m + 1)-го порядку включно, то для будь-якої точки (x, y) із цього околу знайдеться точка
де Pm (x, y) — многочлен Тейлора. Формулу (24) називають формулою Тейлора із залишковим членом у формі Лагранжа. Якщо функція f (x, y) подається у вигляді (23), (24), то говорять, що вона розкладена за формулою Тейлора в околі точки (x 0, y 0). Для функцій трьох і більшої кількості змінних формула Тейлора виводиться аналогічно. Наприклад, для функції z = f (x 1, x 2, x 3, …, xn) у точці
де 1.2.11. Визначник Якобі (якобіан) Важливим формальним засобом дослідження функцій є визначники, утворені з частинних похідних. Нехай дано n функцій n змінних:
які визначені в деякій n -вимірній області D і мають у ній неперервні похідні за всіма змінними. Складемо із цих похідних визначник
Визначник (26) називають функціональним визначником Якобі, або якобіаном, системи функцій (25) за ім’ям німецького математика Якобі, який уперше вивчив його властивості. Позначають якобіан символом
Якобіан має властивості, які подібні до властивостей звичайної похідної. Глибша аналогія між похідними та якобіанами розкривається в теорії неявних функцій, особливо коли йдеться про заміну змінних у кратних інтегралах. 1.2.12. Економічний зміст частинних похідних Нехай задано функцію z = f (x, y). Означення. Частинною еластичністю функції f відносно х називається величина
Частинною еластичністю функції f відносно у називається величина
Інтерпретація. Відсоткове відношення функції наближено дорівнює відсотковому відношенню змінної х з коефіцієнтом Найчастіше в економіці застосовують поняття еластичності попиту. Нехай функції q 1 = f 1(p 1, p 2) i q 2 = f 2(p 1, p 2) виражають попит на товари А і В, що залежать від цін р 1 і р 2 на зазначені товари. Частинні еластичності попиту щодо цін р 1 і р 2 за формулами (27) і (28) набирають вигляду:
Інтерпретація. Частинна еластичність Частинна еластичність
Знайти частинні коефіцієнти еластичностей. ●Маємо
Для цін р 1 = 2, р 2 = 4
Це означає, що коли ціна товару А зростає на 1%, а товару В залишається без змін, то попит на товар знижується на 0,2%. Рівність
відбиває аналогічну залежність: якщо ціна товару В зростає на 1% за незмінної ціни товару А, то попит на цей товар зростає приблизно на 0,2%. Часть I. Общие положения Статья 1. Сфера применения настоящей Конвенции Настоящая Конвенция применяется к последствиям правопреемства государств в отношении государственной собственности, государственных архивов и государственных долгов.
|

 визначає одну зі змінних х або у як неявну функцію іншої змінної. Поданий вираз — це деяке рівняння, що містить х та у і всі члени якого перенесені в ліву частину. Нехай
визначає одну зі змінних х або у як неявну функцію іншої змінної. Поданий вираз — це деяке рівняння, що містить х та у і всі члени якого перенесені в ліву частину. Нехай  . Тоді
. Тоді  . Проте оскільки
. Проте оскільки 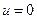 і
і  Звідси
Звідси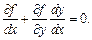 (17)
(17) (вважаючи, що
(вважаючи, що  і
і  існують), знайдемо залежність
існують), знайдемо залежність (18)
(18) Для функції
Для функції  знайти
знайти 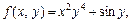

 .
.

 , або
, або  .
. , звідки
, звідки 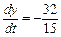 (дм/с).
(дм/с).




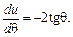




 , (19)
, (19)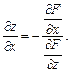 (20)
(20)
 записано
записано  , оскільки згідно з (19) змінна z була спочатку неявною функцією х і у (формулу (20) виведено за припущення, що величина у лишається сталою).
, оскільки згідно з (19) змінна z була спочатку неявною функцією х і у (формулу (20) виведено за припущення, що величина у лишається сталою). . (21)
. (21) . (22)
. (22) . Із рівняння (22) знайдемо значення функції u в точці (1, 1):
. Із рівняння (22) знайдемо значення функції u в точці (1, 1):

 у точці (1, 1, 5) такі:
у точці (1, 1, 5) такі:  ,
, 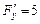 ,
, 
 ,
, 
 (23)
(23)


 ,
, 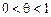 , така що
, така що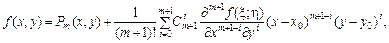 (24)
(24) формула (23) набирає вигляду
формула (23) набирає вигляду ,
,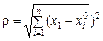 ,
,  і підсумовування викону-
і підсумовування викону- .
. (25)
(25)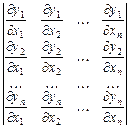 . (26)
. (26) .
. . (27)
. (27) . (28)
. (28) :
: (коли у — величина стала).
(коли у — величина стала).
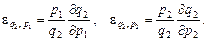
 попиту на товар А щодо ціни р 1 цього товару наближено подає відсоток підвищення (або зниження) попиту на товар А, якщо його ціна зростає на 1%, а ціна товару В лишається незмінною.
попиту на товар А щодо ціни р 1 цього товару наближено подає відсоток підвищення (або зниження) попиту на товар А, якщо його ціна зростає на 1%, а ціна товару В лишається незмінною. попиту на товар А щодо ціни товару В наближено подає відсоток підвищення (зниження) попиту на товар А, якщо ціна товару В зростає на 1%, а товару А залишається без змін.
попиту на товар А щодо ціни товару В наближено подає відсоток підвищення (зниження) попиту на товар А, якщо ціна товару В зростає на 1%, а товару А залишається без змін. Функція попиту на товар А подається у вигляді
Функція попиту на товар А подається у вигляді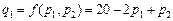 .
. .
. .
.



