Методические указания. Для электрической цепи, изображенной на рис.2.1, выполнить следующее:
Методические указания Расчеты нелинейных электрических цепей могут производиться аналитическим или графическим методом. Аналитический метод расчета нелинейных электрических цепей основан на представлении вольтамперных характеристик (ВАХ) нелинейных элементов (НЭ) уравнениями соответствующих математических функций, позволяющих составить необходимые уравнения, описывающие поведение цепи.
Расчеты нелинейных электрических цепей ведутся большей частью графическим методом, в основу которого положены законы Кирхгофа и вольтамперные характеристики отдельных элементов, входящих в электрическую цепь. Рассмотрим графический метод расчета электрической схемы с двумя последовательно соединенными НЭ, имеющими ВАХ Рис. 3.2. ВАХ нелинейных элементов. Так как при последовательном соединении НЭ через них протекает один и тот же ток I, то строится вспомогательная кривая
б- с параллельным соединением НЭ
При параллельном соединении НЭ, имеющих ВАХ
резистор r3 = 360 Ом.
Рис. 3.4. Схема нелинейной цепи постоянного тока
Напряжение на зажимах цепи U=28 В. Вольтамперные характеристики нелинейных элементов rнэ1 и rнэ2 заданы на рис.3.5 кривыми 1и 2 соответственно. Путем графического расчета определить пределы изменения всех токов и напряжений на участках цепи при изменении приложенного напряжения от 0.5 U до U.
Графический расчет начинается с правой части схемы, содержащей параллельно соединенные элементы rнэ1 и rнэ2. Для этого строятся вольтамперные характеристики нелинейного элемента rнэ2 (зависимость
Рис. 3.5. ВАХ нелинейных элементов: 1-rнэ1, 2-rнэ2 Так как элементы rнэ1 и r3 соединены параллельно, находятся под одним напряжением U2, то графически можно построить вольтамперную характеристику этого участка цепи (зависимость характеристик При этом следует иметь в виду, что ВАХ элемента rнэ2 задана графически на рис. 3.5. кривой 2. ВАХ резистора r3 представляет собой прямую, которая исходит из начала системы координат, а координаты второй точки прямой определяются известным соотношением закона Ома для участка цепи
I1+I2= F(U2) rнэ1 I2=F2(U2)
rнэ2 r3 U2 U2 r3 I3 I3 I2 rнэ2 I2 I1=F1(U1) Iобщ=F(U1+U2)
U1min ΔU1 U1max U2max
U1min ΔU Umax
Рис. 3.6. Графический расчет нелинейной цепи Полученную ВАХ параллельно соединенных элементов rнэ2 и r3 (зависимость рис. 3.5 кривой 1). Нетрудно заметить, что группа элементов rнэ2 и r3 включена последовательно с элементом rнэ1, что позволяет построить эквивалентную ВАХ всей схемы (зависимость Вернувшись в правую часть графического расчета (рис. 3.6) через ВАХ элемента rнэ2 (зависимость Проверка правильности графического расчета осуществляется по законам Кирхгофа. Так должны выполняться следующие соотношения
Проверка по 1-му закону Кирхгофа
Проверка по второму закону Кирхгофа
|

 Решение этих нелинейных уравнений часто приводит к большим трудностям, поэтому аналитический метод, несмотря на все его преимущества, часто уступает место графическому.
Решение этих нелинейных уравнений часто приводит к большим трудностям, поэтому аналитический метод, несмотря на все его преимущества, часто уступает место графическому. и
и  . Графический расчет нелинейной цепи с последовательным соединением НЭ показан на рис. 3.3,а
. Графический расчет нелинейной цепи с последовательным соединением НЭ показан на рис. 3.3,а , абсциссы точек которой находятся суммированием абсцисс соответствующих точек вольтамперных характеристик нелинейных сопротивлений. Наличие этой кривой позволяет по величине напряжения U, приложенного к нелинейной цепи, графически найти ток I, а также напряжения U1и U2 на последовательно соединенных нелинейных сопротивлениях (рис.3.3,а)
, абсциссы точек которой находятся суммированием абсцисс соответствующих точек вольтамперных характеристик нелинейных сопротивлений. Наличие этой кривой позволяет по величине напряжения U, приложенного к нелинейной цепи, графически найти ток I, а также напряжения U1и U2 на последовательно соединенных нелинейных сопротивлениях (рис.3.3,а) Рис. 3.3. Графический расчет нелинейной электрической цепи:а- с последовательным соединением НЭ
Рис. 3.3. Графический расчет нелинейной электрической цепи:а- с последовательным соединением НЭ и
и  строится вспомогательная кривая
строится вспомогательная кривая  , ординаты точек которой находят суммированием ординат соответствующих точек вольтамперных характеристик нелинейных сопротивлений. Наличие этой кривой позволяет при заданной величине напряжения U найти как общий ток, так и токи I1и I2, протекающие через соответствующие нелинейные элементы (рис. 3.3,б)
, ординаты точек которой находят суммированием ординат соответствующих точек вольтамперных характеристик нелинейных сопротивлений. Наличие этой кривой позволяет при заданной величине напряжения U найти как общий ток, так и токи I1и I2, протекающие через соответствующие нелинейные элементы (рис. 3.3,б) Пример Нелинейная цепь, показанная на рис. 3.4, содержит два нелинейных элемента rнэ1 и rнэ2 и
Пример Нелинейная цепь, показанная на рис. 3.4, содержит два нелинейных элемента rнэ1 и rнэ2 и

 ), (показаны на рис. 3.6.)
), (показаны на рис. 3.6.) ) путем суммирования ординат вольтамперных
) путем суммирования ординат вольтамперных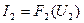 и
и  I,мА I2+I3=F(U2) I,мА
I,мА I2+I3=F(U2) I,мА





 U2min ΔU2
U2min ΔU2  ) путем суммирования абсцисс зависимостей
) путем суммирования абсцисс зависимостей  (ВАХ элемента rнэ1) и
(ВАХ элемента rнэ1) и  , определяем пределы изменения тока
, определяем пределы изменения тока  , через ВАХ элемента rнэ1 (зависимость
, через ВАХ элемента rнэ1 (зависимость  . Пределы изменения
. Пределы изменения  определяются через ВАХ параллельно соединенных элементов rнэ2 и r3(зависимость
определяются через ВАХ параллельно соединенных элементов rнэ2 и r3(зависимость  , а через зависимость
, а через зависимость  .
.




