Задание к расчету.
Задание к расчету. Для магнитной цепи, изображенной на рис. 4.1.
Таблица 4.1
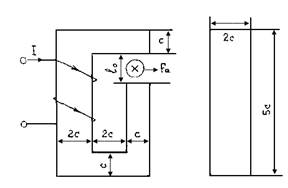
Рис.4.1.
Решение
При расчете полезно составлять расчетные схемы, аналогичные схемам электрических цепей, делающие задачу более наглядной. В этих схемах аналогом ЭДС Е является МДС F, тока I- магнитный поток Ф, напряжения U-магнитное напряжение Uм, сопротивления r- магнитное сопротивление rм. Участки магнитной цепи, выполненные из ферромагнитных материалов, являются нелинейными, а участки, выполненные из немагнитных материалов (например, воздушный зазор), - линейными.
Рис. 4.2 Направление индукции В0 в воздушном зазоре определяется правилом правого буравчика, а направление силы ампера (силы действующей на проводник с током в магнитном поле),- правилом «левой руки». Величина силы Ампера:
Принимая I = 2 A, В = В0 = 1.4 Тл, l = 2 . С = 4 . 10-2 м (I-вариант) Прямая задача На рис. 4.3, а изображена магнитная цепь а=0.12 м, b=0.2 м, с=0.04 м, l0=2.10-3 м. Магнитная индукция в зазоре В0=1.2 Тл. Кривая намагничивания приведена на рис. 4.2. Определить МДС катушки.
Рис.4.3
1. Проводим расчетную силовую линию (показана пунктиром) и разбиваем цепь на участки. Цепь имеет два участка: I-АБВ, выполненный из электротехнической стали, и II-ВА- воздушный зазор. Длина первого участка:
Длина второго участка:
2. Составляем расчетную схему (рис. 4.3, б) 3. Составляем уравнение по второму закону Кирхгофа для магнитной цепи:
Напряженность магнитного поля Н1 первого участка определяем по кривой намагничивания (рис.4.2.) Магнитное напряжение Uм1 на первом участке
Напряженность магнитного поля Н2 в воздушном зазоре определим из выражения:
Магнитное напряжение на воздушном зазоре:
Магнитодвижущая сила катушки:
Обратная задача Для магнитной цепи, рассмотренной в прямой задаче, заданы МДС катушки F=3000 A.Необходимо определить магнитный поток и магнитную индукцию. Так же, как в прямой задаче, разбиваем цепь на участки и составляем расчетную схему. Дальнейшее решение выполняется методом построения вебер-амперных характеристик участков. Магнитная цепь (рис. 4.3, б) содержит два участка: нелинейный (АБВ) и линейный, (ВА) - воздушный зазор. Вебер-амперная характеристика Ф(Uм1) нелинейного участка строится на основе кривой намагничивания (рис. 4.2). Задаемся произвольно значениями магнитной индукции В и по кривой намагничивания определяем соответствующие им значения напряженности магнитного поля Н1 на первом участке. Умножив значения индукции на площадь поперечного сечения, получаем магнитный поток Ф=ВS. Умножив значения напряженности магнитного поля на длину участка, получаем магнитное напряжение на первом участке Таблица 4.2
 второго, линейного участка – прямая – и может быть построена по двум точкам. Одна из этих точек – начало координат, вторая – определяется на основании закона Ома для магнитной цепи второго, линейного участка – прямая – и может быть построена по двум точкам. Одна из этих точек – начало координат, вторая – определяется на основании закона Ома для магнитной цепи
где
Положив, например, На рис. 4.4. показаны вебер – амперные характеристики участков и эквивалентная характеристики всей цепи. Эквивалентная вебер – амперная характеристика цепи Ф(F) строится на основании второго закона Кирхгофа для магнитной цепи путем суммирования абсцисс вебер – амперных характеристик участков.
Отложив по оси магнитных напряжений значение МДС F обмотки, по эквивалентной вебер – амперной характеристике определяем магнитный поток Ф. Из графика видно, что F=3000 A соответствует магнитный поток Ф=22.10-4 Вб. При таком магнитном потоке магнитная индукция
Рис.4.4
|

 При расчете магнитную цепь разбивают на участки. В один участок может быть объединена часть магнитной цепи, по которой проходит один и тот же магнитный поток, выполненная из одного материала и имеющая неизменную площадь поперечного сечения. При этих условиях магнитная индукция
При расчете магнитную цепь разбивают на участки. В один участок может быть объединена часть магнитной цепи, по которой проходит один и тот же магнитный поток, выполненная из одного материала и имеющая неизменную площадь поперечного сечения. При этих условиях магнитная индукция 
 и напряженность магнитного поля
и напряженность магнитного поля  в пределах участка имеют неизменные значения. Длины участков определяются по расчетной (средней) силовой линии. Расчет неразветвленных магнитных цепей ведется на основе второго закона Кирхгофа для магнитных цепей (закон полного тока).
в пределах участка имеют неизменные значения. Длины участков определяются по расчетной (средней) силовой линии. Расчет неразветвленных магнитных цепей ведется на основе второго закона Кирхгофа для магнитных цепей (закон полного тока).









 Результаты расчета сводим в табл.4.2.
Результаты расчета сводим в табл.4.2.




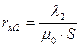 -магнитное сопротивление второго участка (воздушного зазора);
-магнитное сопротивление второго участка (воздушного зазора);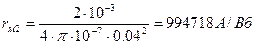
 , получим
, получим 





