Наращение сложных процентов
В среднесрочных и долгосрочных финансово-кредитных операциях, если проценты не выплачиваются сразу же после их начисления, а присоединяются к сумме ссуды, для подсчета наращенной суммы применяются сложные проценты. База для начисления сложных процентов увеличивается с каждым периодом начисления (процентным периодом). В конце первого периода к исходной сумме P прибавляется сумма процентов, начисленных за этот период, P × i. Наращенная сумма в конце первого периода S1 будет равна [2]: S1 = P + P × i = P × (1 + i). В конце второго периода наращенная сумма S2 составит S2 = S1 × (1 + i) = P × (1 + i) × (1 + i) = P × (1 + i) 2. Аналогично, к концу третьего периода наращенная сумма составит S3 = S2 × (1 + i) = (1 + i) × P × (1 + i) 2 = P × (1 + i) 3. В общем случае к концу n -го периода наращенная сумма: Sn = Sn-1 × (1 + i) = (1 + i) × P × (1 + i) n-1 = P × (1 + i) n. (2.1) Множитель (1 + i) n называется множителем наращения. При выводе формулы (2.1) предполагалось, что число периодов n является целым, хотя на практике часто приходится вычислять суммы, наращенные за нецелое число периодов начисления. По определению для произвольного (возможно, нецелого) числа периодов t наращенная сумма рассчитывается по общей формуле: St = P × (1 + i) t. (2.2) Задача №8. Банк начисляет ежегодно 8% сложных. Клиент положил в этот банк 20000 рублей. Какая сумма будет на его счете: а) через 5 лет; б) через 6 лет и 3 месяца? Сравнить полученную сумму с наращенной суммой, которая могла быть получена в случае выплаты простых процентов. Решение. Применяя базовую формулу (2.2), находим наращенную сумму S для сложных процентов при а) P = 20000 руб., i = 0,08, t = 5: S = 20000 × (1 + 0,08) 5 = 20000 × 1,469328 = 29386,56 руб. При расчете простых процентов при заданных исходных данных наращенная сумма равна: S = 20000 × (1 + 0,08 × 5) = 20000 × 1,4 = 28000 руб. б) P = 20000 руб., i = 0,08, t = 6,25: S = 20000 × (1 + 0,08) 6,25 = 20000 × 1,617702 = 32354,04 руб. При расчете простых процентов при заданных исходных данных наращенная сумма S = 20000 × (1 + 0,08 × 6,25) = 20000 × 1,5 = 30000 руб. Реализовать приведенные выше вычисления с помощью Excel, используя в формулах встроенную математическую функцию СТЕПЕНЬ.
Как правило, ставка сложных процентов указывается на период, равный году, но начисление сложных процентов может производиться каждое полугодие, квартал, месяц или даже день. При этом за каждый такой период, равный 1 / m части года, начисляются сложные проценты по ставке i / m сложных процентов, т.е. формула (2.2) примет следующий вид [2]:
где t - длительность промежутка времени, в течение которого начисляются сложные проценты (измеряется в годах). Например, в случае одного квартала t = 0,25. Чтобы показать, что при годовой ставке сложных процентов i начисление сложных процентов производится m раз в год по ставке i / m, эту ставку обозначают как jm. Тогда формула (2.3) преобразуется к виду:
Задача №9. Решить предыдущую задачу при j4 = 8% и j12 = 8%. Решение. Применяя формулу (2.4), находим наращенную сумму S для сложных процентов при j4 = 8%:
Наращенная сумма S для сложных процентов при j12 = 8% будет равна:
Решение применительно к случаю б) задачи №1 получить самостоятельно. Использовать в расчетах возможности Excel. Примечание. Из приведенных выше расчетов видно, что при увеличении числа периодов начисления процентов при той же годовой процентной ставке наращенная сумма, полученная за одно и то же время, увеличивается.
Как отмечалось выше, дисконтирование - это операция обратная наращению. Дисконтирование по ставке сложных процентов, когда проценты начисляются m раз в году, осуществляется следующим образом [3]:
D = S – P. (2.6) В этом случае величина P называется современной стоимостью S, а величина D - дисконтом. Задача №10. Гражданин Смирнов может вложить деньги в банк, выплачивающий j12 =7%. Какую сумму ему следует вложить, чтобы получить 3000 рублей через 4,5 года? Реализовать вычисления с помощью Excel, используя в формуле встроенную математическую функцию СТЕПЕНЬ. Задача №11. Гражданин Буйнов хочет вложить 5000 рублей в банк, чтобы через 2 года получить 7000 рублей. Под какую процентную ставку j4 он должен вложить свои деньги? Реализовать вычисления с помощью Excel, используя в формуле встроенную математическую функцию СТЕПЕНЬ. Задача №12. Определить годовую ставку начисляемых ежегодно процентов, если вложенная сумма денег удваивается через 8 лет.
Контрольные вопросы ü Каким образом происходит наращение денежной суммы, взятой в долг, при использовании простого процента. ü Что такое дисконт. ü Каким образом происходит наращение денежной суммы, взятой в долг, при использовании простого процента. ü Как изменяется наращение суммы долга при неизменных ставке сложного процента и общем сроке при уменьшении периода наращения.
|

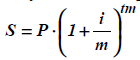 (2.3)
(2.3)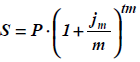 (2.4)
(2.4)

 (2.5)
(2.5)


