Требования МНК1. Математическое ожидание случайного отклонения
2. Гомоскедастичность (постоянство дисперсии отклонений):
3. Отсутствие автокорреляции. Случайные отклонения
4. Случайное отклонение должно быть независимо от объясняющих переменных.
5. Модель является линейной относительно параметров. Для случая множественной линейной регрессии существенными являются еще два требования. 6. Отсутствие мультиколлинеарности. Между объясняющими переменными отсутствует строгая (сильная) линейная зависимость. 7. Ошибки Выполнение данного требования важно для проверки статистических гипотез и построения интервальных оценок. Представим выражение (3) в матричной форме:
Здесь
В этой матрице -я строка Вывод и интерпретация коэффициентов множественной регрессии
|
равно нулю для всех наблюдений:
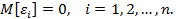
для любых наблюдений i и j.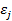
являются независимыми друг от друга для всех 
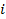и 
.
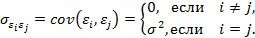
б имеют нормальное распределение 
.
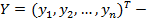вектор-столбец значений зависимой переменной, Т – символ транспонирования, 
вектор-столбец (размерности m+ 1) неизвестных коэффициентов регрессии, 
вектор-столбец случайных отклонений,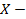 
матрица размерности 
:
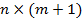представляет наблюдение вектора значений независимых переменных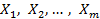 
; единица соответствует переменной при свободном члене 
.
