Модель с двумя независимыми переменнымиОбобщением линейной регрессионной модели с двумя переменными является многомерная регрессионная модель (или модель множественной регрессии). Уравнение множественной регрессии может быть представлено в виде
где Рассмотрим самую употребляемую и наиболее простую модель множественной регрессии – модель множественной линейной регрессии. Теоретическое линейное уравнение регрессии имеет вид:
или для индивидуальных наблюдений
Здесь Если число наблюдений В данном случае число Наиболее распространенным методом оценки параметров уравнения множественной регрессии является метод наименьших квадратов (МНК).
|
вектор независимых (объясняющих) переменных; вектор параметров (подлежащих определению); 
случайная ошибка (отклонение); 
зависимая (объясняемая) переменная.
вектор размерности 
неизвестных параметров. 
называется j -м теоретическим коэффициентом регрессии (частичным коэффициентом регрессии). Он отражает влияние на условное математическое ожидание 
зависимой переменной 
объясняющей переменной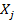 
при условии, что все другие объясняющие переменные модели остаются постоянными. 
свободный член, определяющий значение 
, то существует бесконечно много различных векторов параметров, при которых линейная формула (3) связи между X и Y будет выполняться абсолютно точно. Если число наблюдений 
, то вектор β рассчитывается единственным образом. При 
возникает необходимость оптимизации, т.е. оценивания параметров 
при которых формула (3) дает наилучшее приближение для имеющихся наблюдений.
называется числом степеней свободы.
