Выборочные характеристики.
1. Получите две выборки объемом 80 и 60 значений из нормально распределенных генеральных совокупностей с разными значениями параметров с помощью стандартного средства Excel Сервис\Анализ данных\Генерация случайных чисел. В отсутствие данного пункта в меню необходимо в Надстройках указать Пакет анализа, после чего Анализ данных должен стать доступным в меню Сервис. (В дальнейшем, в результате применения различных описательных статистик, в том числе гистограмм, надо будет обнаружить наличие неоднородности в изучаемой объединенной выборке, однако различия не должны быть очевидными сразу) Для того чтобы с помощью Сервис\Анализ данных\Генерация случайных чисел получить выборку из нормального распределения необходимо заполнить соответствующие поля: Число переменных — поле, указывающее число выводимых столбцов данных; если необходимо получить значения только в одном столбце, то это поле можно оставить пустым; Число случайных чисел — объем выборки; Распределение — тип распределения: выберите в списке Нормальное и укажите его Параметры: математическое ожидание и среднее квадратическое отклонение (выберите произвольно); Случайное рассеивание — это поле можно оставить пустым; Параметры вывода — в поле Выходной интервал укажите адреса диапазона, состоящего из нужного количества ячеек, в которые будут выведены значения (можно указать только адрес первой ячейки — в этом случае все остальные значения будут записаны ниже в том же столбце). 2. По объединенной выборке, моделирующей выборку из конечной смеси двух распределений, составьте вариационный ряд(выборку, упорядоченную по возрастанию значений). Для этого скопируйте значения, вставьте на свободное место рабочего листа и упорядочьте по возрастанию, например с помощью сортировки. 3. Найдите выборочные характеристики (в скобках указаны имена необходимых функций, аргументом которых является диапазон, содержащий выборку): – наибольшее значение – наименьшее значение – объем выборки – выборочную среднюю – медиану: значение, которое делит вариационный ряд на две равные (по числу значений) части (МЕДИАНА); – моду: наиболее часто встречающееся значение (МОДА); – вариационный размах – исправленную (несмещенную) выборочную дисперсию (ДИСП); – дисперсию (смещенную) выборки (ДИСПР); – выборочное среднее квадратическое отклонение, вычисленное по исправленной (несмещенной) выборочной дисперсии (СТАНДОТКЛОН); – выборочное среднее квадратическое отклонение, вычисленное по смещенной выборочной дисперсии (СТАНДОТКЛОНП); – среднее абсолютное отклонение от выборочного среднего (СРОТКЛ); – эксцесс эмпирического распределения: значение, характеризующее форму кривой распределения (ЭКСЦЕСС); – асимметрию эмпирического распределения: значение, характеризующее форму кривой распределения (СКОС); – коэффициент вариации, равный выборочному среднему квадратическому отклонению, деленному на выборочную среднюю (коэффициент вариации обычно выражается в процентах); – ошибку выборки, равную среднему квадратическому отклонению, деленному на корень из числа наблюдений. (Можно ли по вычисленным значениям описательных статистик сделать обоснованное предположение о присутствии заметной неоднородности в объединенной выборке.) 4. Эти же значения определите с помощью стандартных средств Excel Сервис\Анализ данных\Описательная статистика. Не забудьте отметить поле Итоговая статистика и разместите результаты расчета на том же листе. 5. Постройте гистограмму частот распределения значений показателя. Сначала необходимо разбить диапазон изменений показателя на конечное число Для подсчета частот попадания значений показателя в интервалы разбиения используется функция ЧАСТОТА,являющаяся функцией массива. Поэтому сначала необходимо выделить ячейки, в которых будут записаны найденные частоты (в нашем случае 6 ячеек — на единицу больше, чем число интервалов), вставить функцию, используя мастер функций, поставить курсор в строку формул (или нажать F2) и ввести функцию в выделенные ячейки с помощью нажатия (одновременного!) Ctrl+Shift+Enter. Аргументами функции ЧАСТОТА являются: Массив_данных — весь интервал ячеек, в которых содержится выборка; Двоичный_массив — адреса ячеек, в которых содержатся значения правых границ интервалов разбиения (группировки). В результате в выделенных ячейках будет получено шесть чисел, первое из которых равно числу значений выборки, попавших в 1-й интервал, второе — попавших во 2-й интервал и т.д. Последнее число часто используется для контроля и равно числу значений, больших правой границы последнего интервала (в нашем случае равной 21). Очевидно, что оно должно быть равно 0. Сумма значений полученных частот должна быть равна объему выборки По найденным значениям частот на одной диаграмме постройте гистограмму. 6. Вычислите относительные частоты попадания в каждый интервал разбиения. Относительная частота По найденным значениям относительных частот на второй диаграмме постройте гистограмму относительных частот.
7. Определите плотности относительных частот, равные значениям относительных частот, деленных на длину интервала разбиения: (Можно ли по построенным гистограммам сделать обоснованное предположение о наличии существенной неоднородности в объединенной выборке) 8. Подсчитайте кумулятивные (интегральные) частоты. Значение кумулятивной частоты для интервала представляет собой сумму частот текущего и всех предыдущих интервалов (накопленные частоты): 9. Вычислите относительные кумулятивные частоты, которые равны кумулятивным частотам, деленным на число элементов выборки: 10. Постройте на отдельном листе гистограмму распределения частот и график интегральных частот для выбранных семи интервалов разбиения исходного диапазона с помощью стандартных средств Excel Сервис\Анализ данных\Гистограмма. Для того чтобы построить диаграмму для семи интервалов (карманов) разбиения необходимо в поле Интервал карманов указать адреса ячеек, содержащих правые границы интервалов разбиения. 11. Постройте соответствующие таблицы и графики для разных чисел интервалов разбиения исходного диапазона: а) для 10 интервалов разбиения; б) для числа интервалов, вычисленного по формуле 12. Оформите отчет, в котором приведите результаты расчетов в виде таблиц и диаграмм, указанных в перечисленных пунктах. Сделайте обоснованный вывод о наличии существенной неоднородности в исходных данных.
|

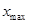 (МАКС);
(МАКС); (МИН);
(МИН);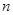 (СЧЕТ);
(СЧЕТ);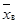 (СРЗНАЧ),
(СРЗНАЧ), (размах выборки): разница между наибольшим и наименьшим значениями выборки,
(размах выборки): разница между наибольшим и наименьшим значениями выборки,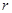 непересекающихся интервалов
непересекающихся интервалов  и для каждого из них подсчитать частоту попаданий значений показателя
и для каждого из них подсчитать частоту попаданий значений показателя  (т.е. число значений объединенной выборки, попавших в интервал). Результаты последующих вычислений удобно сгруппировать в таблицу, в которой кроме названий интервалов разбиения и их правых границ следует также указать середины интервалов разбиения. Пусть минимальное значений выборки равно 1, а максимальное — 21. Тогда размах выборки равен
(т.е. число значений объединенной выборки, попавших в интервал). Результаты последующих вычислений удобно сгруппировать в таблицу, в которой кроме названий интервалов разбиения и их правых границ следует также указать середины интервалов разбиения. Пусть минимальное значений выборки равно 1, а максимальное — 21. Тогда размах выборки равен  . Разобьем весь диапазон на
. Разобьем весь диапазон на 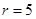 интервалов равной длины
интервалов равной длины  . Следовательно, правым границам интервалов разбиения соответствуют числа 5, 9, 13, 17, 21, а серединам интервалов — числа 3, 7, 11, 15, 19.
. Следовательно, правым границам интервалов разбиения соответствуют числа 5, 9, 13, 17, 21, а серединам интервалов — числа 3, 7, 11, 15, 19. равна значению соответствующей частоты, деленной на число элементов выборки (в нашем случае 100):
равна значению соответствующей частоты, деленной на число элементов выборки (в нашем случае 100):  . Сумма значений полученных относительных частот должна быть равна 1.
. Сумма значений полученных относительных частот должна быть равна 1. . По найденным значениям на одном графике постройте гистограмму и полигон плотности относительных частот.
. По найденным значениям на одном графике постройте гистограмму и полигон плотности относительных частот.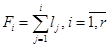 . Так, например, значение кумулятивной частоты для интервала 9–13 равно числу элементов выборки, меньших 13. Поэтому первое значение кумулятивной частоты просто равно первому значению частоты, например 10, а каждое ее значение для следующего интервала получается сложением предыдущего значения кумулятивной частоты со значением частоты для этого интервала. Второе значение кумулятивной частоты 30 равно сумме предыдущего значения кумулятивной частоты 10 и второго значения частоты 20 и т.д.
. Так, например, значение кумулятивной частоты для интервала 9–13 равно числу элементов выборки, меньших 13. Поэтому первое значение кумулятивной частоты просто равно первому значению частоты, например 10, а каждое ее значение для следующего интервала получается сложением предыдущего значения кумулятивной частоты со значением частоты для этого интервала. Второе значение кумулятивной частоты 30 равно сумме предыдущего значения кумулятивной частоты 10 и второго значения частоты 20 и т.д.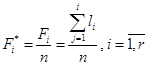 . По найденным значениям постройте гистограмму и полигон относительных кумулятивных частот. Значения относительных кумулятивных частот фактически представляют собой эмпирическую функцию распределения. Запишите полученную функцию аналитически.
. По найденным значениям постройте гистограмму и полигон относительных кумулятивных частот. Значения относительных кумулятивных частот фактически представляют собой эмпирическую функцию распределения. Запишите полученную функцию аналитически.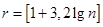 . Здесь квадратные скобки означают целую часть числа,
. Здесь квадратные скобки означают целую часть числа,  — объем выборки. Эта формула в большинстве случаев дает хорошую оценку оптимального числа интервалов разбиения. Сравните полученные результаты и выберите наиболее удачное в данном случае разбиение.
— объем выборки. Эта формула в большинстве случаев дает хорошую оценку оптимального числа интервалов разбиения. Сравните полученные результаты и выберите наиболее удачное в данном случае разбиение.


