История болезни
"Чисельне обчислення значення визначеного інтегралу"; Привести алгоритми та скласти ПЕОМ-програму для обчислення згідно номеру варіанта значення визначеного інтегралу методами лівих прямокутників, правих прямокутників, трапецій та Симпсона, прийняв Привести алгоритми та скласти ПЕОМ-програму для обчислення даного інтегралу методом подвійного перерахунку з заданою заздалегідь похибкою для варіантів 1, 5, 9, 13, 17, 21, 25 – лівих прямокутників; для варіантів 2, 6, 10, 14, 18, 22, 26 – правих прямокутників; для варіантів 3, 7, 11, 15, 19, 23, 27 – трапецій. для варіантів 4, 8, 12, 16, 20, 24, 28 – Симпсона. 1.
2.
3.
4.
5. 6.
7.
8.
9.
10.
11.
12.
13.
14.
15. 16.
17.
18.
19.
20. 21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
Лабораторна робота №5 «Численное решение нелинейных уравнений с одной переменной». Задание: Дано нелинейное уравнение согласно номеру варианта. 1. Определить один из отрезков изоляции корня заданного уравнения графически и с помощью ЭВМ (методом табулирования). 2. Составить ЭВМ-программу для вычисления (уточнения) корня уравнения на найденном отрезке. Задачу решить с помощью следующих методов: половинного деления; хорд; касательных; последовательных приближений. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28.
29.
30.
ГРОДНЕНСКИЙ ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ КАФЕДРА ДЕТСКОЙ ХИРУРГИИ ЗАВ. КАФЕДРОЙ д.м.н., проф. Ковальчук РУКОВОДИТЕЛЬ ГРУППЫ к.м.н., доц. Иодковский К. М.
История болезни Больной:Лавыш Максим Юрьевич Клинический диагноз: Варикоцеле слева 2 степени
|

 30.
30. в рамках методу:
в рамках методу: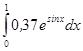 .
. .
. .
. .
. .
. .
. .
. .
. .
.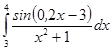 .
. .
. .
. .
. .
. .
.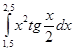 .
. .
. .
.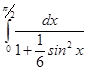 .
.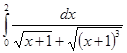 .
. .
. .
.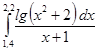 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.



