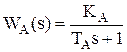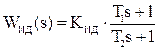Дифференциальные уравнения динамических звеньев первого порядка и их решения
1. Автобусный парк (автобусы; сотрудники, включая водителей; междугородние маршруты); 2. Суд (участники процессов, залы заседаний, дела); 3. Аптека (сотрудники, лекарства, лекарства-заменители); 4. Аэропорт (экипаж, самолёт, расписание, маршрут, задержки); 5. Кафе (сотрудники, напитки, еда, поставщики); 6. Библиотека (книги, читатели); 7. Бюро расписаний; 8. ГИБДД (автомобили, водители, ДТП); 9. Агентство недвижимости (клиенты, недвижимость); 10. Биржа труда (работодатели; люди, ищущие работу); 11. Гостиница (номера, клиенты, горничные); 12. Детский сад (ребёнок, сотрудник); 13. ЖЭУ (сотрудники, жилищный фонд, заявки, оплата); 14. Отдел кадров (сотрудники, командировки, отделы); 15. Поликлиника (врач, пациент, медицинская карта); 16. Прокат автомобилей (клиент, автомобиль, сотрудник). Дифференциальные уравнения динамических звеньев первого порядка и их решения К динамическим звеньям первого порядка относятся: идеальное и реальное интегрирующие звенья, апериодическое, реально-дифференцирующее и интегро-дифференцирующее звенья [3]. В идеальном интегрирующем звене выходная величина
где: Решением уравнения (4.1.1) при нулевых начальных условиях является:
Передаточная функция идеально - интегрирующего звена имеет вид:
Реальное интегрирующее звено описывается дифференциальным уравнением, имеет передаточную функцию и решение дифференциального уравнения, которые запишутся соответственно:
где: Дифференциальное уравнение, передаточная функция апериодического звена и его решение запишутся соответственно:
Для реального дифференцирующего звена можно записать:
Интегро-дифференцирующее звено имеет дифференциальное уравнение и передаточную функцию, соответственно:
Меняя коэффициенты модели Структурные схемы рассматриваемых звеньев первого порядка, их передаточные функции и соотношения параметров схем приведены в таблице 4.1.1. Динамические свойства звеньев и систем определяются с помощью временных и частотных характеристик. Временные характеристики показывают изменение во времени выходного сигнала исследуемого звена или системы при подаче на вход типового входного сигнала при нулевых начальных условиях. Различают следующие временные характеристики: переходнуюфункцию (характеристику) [ h(t) ] – реакция звена или системы на единичное ступенчатое воздействие и импульсную переходную или весовую функцию - Частотные характеристики определяют реакцию звена или системы на гармонический входной сигнал.
Переходная функция может быть определена как обратное преобразование Лапласа изображения выходной величины:
здесь Но так как интеграл (4.1.7) является не берущимся, то для определения выражения
где: В, А – числитель и знаменатель передаточной функции; Звено будет устойчивым, если переходный процесс при Приведенная формула Хевисайда применима, если корни характеристического уравнения простые и не нулевые. Таблица 4.1.1
Продолжение таблицы 4.1.1
|

 пропорциональна интегралу от входной величины
пропорциональна интегралу от входной величины  и определяется выражением:
и определяется выражением: , (4.1.1)
, (4.1.1)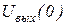 – начальное значение выходной величины.
– начальное значение выходной величины. (4.1.2)
(4.1.2) .
.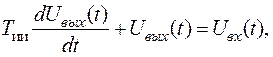
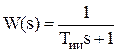 ,
, , (4.1.3)
, (4.1.3) – корень характеристического уравнения звена (
– корень характеристического уравнения звена ( );
);  – амплитуда ступенчатого воздействия.
– амплитуда ступенчатого воздействия. ,
, ,
, . (4.1.4)
. (4.1.4) ,
, ,
, ,
,  . (4.1.5)
. (4.1.5)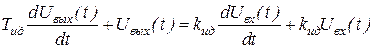 ,
, . (4.1.6)
. (4.1.6) ,
,  ,
,  интегро–дифференцирующего звена (4.1.6) можно реализовать пропорциональное звено; звено с преобладанием функций дифференцирования, интегрирования; идеальное интегрирующее; реальное интегрирующее звено и т.д. [3].
интегро–дифференцирующего звена (4.1.6) можно реализовать пропорциональное звено; звено с преобладанием функций дифференцирования, интегрирования; идеальное интегрирующее; реальное интегрирующее звено и т.д. [3]. (t) – реакция на единичное импульсное воздействие.
(t) – реакция на единичное импульсное воздействие.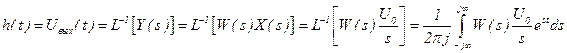 (4.1.7),
(4.1.7),
 – изображение по Лапласу ступенчатого входного сигнала с амплитудой U0.
– изображение по Лапласу ступенчатого входного сигнала с амплитудой U0.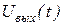 можно воспользоваться формулой Хевисайда:
можно воспользоваться формулой Хевисайда: , (4.1.8)
, (4.1.8) – i – тое значение корня характеристического уравнения.
– i – тое значение корня характеристического уравнения. стремится к установившемуся значению
стремится к установившемуся значению 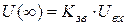 .
.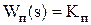




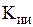 =1 (10, 100)
=1 (10, 100)