Использование подпрограмм и модулей
Цель работы – приобретение навыков программирования при решении задач с использованием подпрограмм и модулей. 6.1 Подпрограмма-функция и подпрограмма-процедура При программировании часто возникает необходимость повторять одну и ту же последовательность операторов в различных частях программы при разных параметрах, многократно переписывая их. Для реализации таких действий и сокращения объема программы удобно использовать подпрограммы: процедуры и функции. При решении задач с использованием подпрограмм необходимо сначала определить, что будет вычисляться многократно и сколько при одном вычислении будет результатов. Затем выбрать тип используемой подпрограммы в зависимости от количества предполагаемых результатов, т.к. в подпрограмме-функции результат может быть только один, а подпрограмме-процедуре несколько. Любая подпрограмма содержит: - заголовок; - описательную часть; - исполнительную часть. Заголовок подпрограмм оформляется по следующим правилам:
Параметры, которые используются в описании процедуры, называются формальными (глобальными) параметрами. Формальные параметры процедуры делятся на параметры-значения и параметры-переменные. Под параметрами-значениями понимаются параметры, значения которых не меняются в ходе выполнения подпрограммы (входные). Параметры-переменные - выходные величины подпрограммы, значения которых передаются в головную программу. В списке формальных параметров перед перечислением параметров-переменных необходимо поставить слово Var. В рассмотренном примере вещественная величина max и целая i являются параметрами переменными. Параметры-значения в примере представлены целой величиной N и вещественными A и B. Если в подпрограмме будет использоваться параметр нестандартного типа, например массив, то этот тип должен быть описан явным способом в головной программе. Формальные параметры подпрограммы-функции могут быть только параметрами-значениями, т.е. входными данными, а выходным параметром является имя подпрограммы, поэтому в заголовке необходимо указать ее тип. Таким образом, результат процедуры передается через параметры-переменные, а результат подпрограммы-функции через ее имя. В связи с этим имя функции используется в качестве переменной в исполнительной части подпрограммы, которой присваивается результат, а для процедуры это категорически запрещается. В описательной части подпрограммы следует описать локальные переменные (т.е. те, что используются только внутри подпрограммы), формальные параметры в этой части подпрограммы уже не описываются. Исполнительная часть подпрограммы реализует алгоритм, вынесенный в нее. Для подпрограммы-функции в этой части должен присутствовать оператор присваивания, в левой части которого стоит имя функции. В отличие от программы подпрограмма заканчивается точкой с запятой. Обращение к подпрограмме осуществляется из головной программы по следующим правилам:
Параметры, которые при обращении к подпрограмме подставляются вместо формальных, называются фактическими (локальными) параметрами. Соответствие между фактическими и формальными параметрами устанавливается согласно порядку их следования, количеству в списке и в соответствии с указанным типом. В программе может содержаться несколько различных подпрограмм, которые располагаются одна за другой после совокупности описания переменных головной программы. Если какая-то подпрограмма обращается к другой подпрограмме, то вызывающая подпрограмма должна располагаться после вызываемой.
6.2 Использование модулей Кроме процедур и функций в Паскале используются модули. Библиотечный модуль – это самостоятельно компилируемый файл Turbo Pascal, который может содержать описания констант, переменных, типов, процедур и функций. После того, как модуль создан и откомпилирован, его ресурсы можно использовать в любой программе на Turbo Pascal, просто указав имя этого модуля. Подпрограмму включают в состав модуля в том случае, когда она реализует действие, которое приходится выполнять достаточно часто. Такую подпрограмму можно написать и отладить один раз, а использовать многократно. Файл, содержащий модуль, обязан иметь имя, совпадающее с именем модуля. Доступ из программы к функциям модуля обеспечивает оператор использования Uses, который размещается сразу после заголовка программы и в котором указывается имя модуля (или нескольких модулей). В самой первой строке модуля находится директива компилятору. Директива начинается со знака $ и заключается в фигурные скобки, причем между открывающей фигурной скобкой и знаком $ не должно быть пробела. Директива позволяет изменить работу (транслятора) компилятора – например, на необходимость использования программой математического сопроцессора. Каждый модуль имеет секции, озаглавленные зарезервированными словами. Модуль начинается с зарезервированного слова Unit, за которым указывается заголовок модуля, и заканчивается словом End (признаком конца модуля), за которым следует точка. Для этого End не требуется соответствующего слова Begin, так как Begin служит признаком начала инициирующей секции, существование которой в модуле необязательно. Таким образом, парой слову End служит слово Unit, а не Begin. Секция Interface (интерфейсная секция) содержит описания констант, типов, переменных и процедур, доступных из вызывающей программы или модуля, и обеспечивает взаимодействие модуля с другими модулями, а также с основной программой. Секция Implementation (секция реализации) содержит исходный код программ, заголовки которых представлены в интерфейсной секции модуля, а также может содержать локальные по отношению к модулю описания. Модуль следует обязательно оттранслировать, при этом появится файл, имя которого совпадает с именем исходного файла, а расширение имеет вид .tpu. Выполнить оттранслированный модуль нельзя. В состав Turbo Pascal 7.0 входит набор из восьми стандартных модулей (System, Dos, Crt, Printer, Graph, Overlay, Turbo3 (Graph3) и Strings), содержащих множество предопределенных типов, констант, переменных, процедур и функций, которые без ограничений можно использовать в пользовательских программах. Полное описание библиотечных модулей можно найти в файле помощи Help интегрированной инструментальной оболочки Turbo Pascal 7.0. Модуль System – это основное хранилище Turbo Pascal, в котором содержатся подпрограммы поддержки всех встроенных возможностей языка программирования, таких как файловый ввод-вывод, обработка строк, целочисленная арифметика, арифметика с плавающей точкой и динамическое распределение памяти. В отличие от других модулей этот модуль не требуется указывать в разделе Uses программы. В модуле Dos собраны процедуры и функции, а также переменные и константы, позволяющие из программ получать доступ к средствам MS DOS и управлять файлами. Подпрограммы модуля Crt позволяют управлять текстовыми режимами экрана, его цветами и окнами, яркостью свечения символов, а также расширенными кодами клавиатуры и звуком. В модуле Printer объявляется только файловая переменная Lst, имеющая тип Text, которая ассоциируется с системным устройством LPT и позволяет выводить данные на печать. Модуль Graph содержит множество подпрограмм, предназначенных для управления графическим режимом экрана. Однако для запуска программы, использующей этот модуль, необходимо иметь графический драйвер (файл с расширением .bgi) и, в дополнение к нему, файлы шрифтов (с расширением .chr). При разработке крупных программ, когда возникает необходимость разбиения программы на отдельные сегменты (оверлеи), используют специальные средства, которые содержатся в модуле Overlay. Модули Turbo3 и Graph3 предназначены для поддержания совместимости с Turbo Pascal 3.0, которая в настоящее время практически не используется. Модуль Strings содержит функции и процедуры для написания программ, совместимых с Windows-приложениями.
6.3 Примеры использования подпрограмм и модулей 6.3.1 Вычислить На рисунке 6.1 представлена блок-схема алгоритма решения задачи с использованием двух подпрограмм-процедур. В приведенной ниже программе решения данной задачи использованы две процедуры - VV и SUM. Первая служит для ввода значений исходных матриц и вызывается в основной программе после ввода значений размерностей массивов A и B – n и m. Входными данными процедуры VV являются величина k, определяющая размерность вводимой матрицы. Выходные параметры, передаваемые в программу, - элементы массива Х. При первом вызове процедуры VV формальные параметры k, Х соответственно заменяется фактическими параметрами n, A. Подобная замена формальных параметров фактическими осуществляется и при втором вызове подпрограммы.
На рисунке 6.2 представлена блок-схема алгоритма решения этой же задачи другим способом – с использованием подпрограммы-функции.
В приведенной ниже программе вызов реализован второй вариант решения данной задачи, в котором вместо процедуры SUM введена вещественная функция SUM. Такая замена повлекла соответствующие изменения как в описании подпрограммы, так и в обращении к ней. Вызов подпрограммы SUM осуществляется в головной программе после ввода элементов исходных массивов. Входные параметры – массив Х и его размер k, выходной параметр - сумма элементов массива S. Следует отметить, что используемый в процедурах параметр i является локальным, то есть сохраняющим свои значения только внутри процедуры. После выполнения подпрограммы значения локальных параметров забываются. Поскольку процедура SUM имеет только один выходной параметр, то вместо нее можно использовать подпрограмму-функцию.
6.3.2 Создать модуль, содержащий описания гиперболических функций Sinh(x), Cosh(x) и Tanh(x), используя известные математические соотношения
Ниже приведен текст созданного модуля и программа проверки, использующая его. {$N+} { директива компилятору } Unit hyp_fun; { заголовок модуля } Interface { интерфейсная секция } Function sinh (x: extended): extended; Function cosh (x: extended): extended; Function tanh (x: extended): extended; Implementation { секция реализации } var t: extended; Function sinh (x: extended): extended; Begin t:= exp(x); sinh:= 0.5*(t – 1.0/ t); End; Function cosh (x: extended): extended; Begin t:= exp(x); cosh:= 0.5*(t + 1.0/ t); End; Function tanh (x: extended): extended; Begin t:= exp(x); tanh:= (t - 1.0) / (t + 1.0); End; End. { конец модуля }
{$N+} Program Test_hyperbolic_fun; {программа проверки} Uses hyp_fun; Begin Writeln (‘sinh (0.5) =’, sinh (0.5)); Writeln (‘cosh (-0.5) =’, cosh (-0.5)); Writeln (‘tanh (1.5) =’, tanh (1.5)); Write (‘Нажмите <Enter>:’); Readln; End.
6.4 Варианты заданий 6.4.1 Использование подпрограммы-функции 1 Вычислить значение функции 2 Даны массивы С(10), D(15) и вещественное число Х. Вычислить значение функции Z=AX2+B, где 3 Вычислить среднее арифметическое элементов каждого из массивов Х(10), У(15), Z(20). 4 Определить порядковые номера минимальных элементов массивов Z(10) и X(15). 5 Вычислить суммы элементов, расположенных на главных диагоналях каждой из матриц А(5,5) и В(7,7). 6 Найти сумму положительных элементов в каждом из массивов Y(3,6) и Х(5,4). 7 Вычислить среднее арифметическое элементов, расположенных на главной диагонали, для каждой из матриц А(4,4) и С(5,5). 8 Вычислить значение функции 9 Найти количество элементов больших 7 в матрицах А(3,5) и В(4,4). 10 Вычислить среднее арифметическое элементов, расположенных выше главной диагонали, для матриц А(5,5) и В(7,7). 11 Вычислить значение функции 12 Вычислить значение функции Y=ax2+bx+c, где х - заданное число, 13 Найти сумму наименьших элементов матриц C(9) и D(10). 14 Определить среднее геометрическое минимальных элементов массивов Х(10) и Y(15). 15 Найти произведение наименьших элементов матриц А(10) и В(12). 16 Вычислить произведение элементов, расположенных на главных диагоналях, для каждой из матриц А(5,5) и В(7,7). 17 Определить количество элементов, попадающих в интервал [-2, 6], для каждого из массивов А(10) и В(15). 18 Вычислить среднее арифметическое элементов, расположенных ниже главной диагонали, для каждой из матриц А(4,4) и С(5,5). 19 Найти количество элементов меньших 10 в матрицах А(3,5) и В(4,4). 20 Даны число х и одномерные массивы С(10) и D(15). Вычислить 21 Определить количество нулевых элементов в каждом из массивов А(10) и В(13). 22 Найти произведение отрицательных элементов в каждом из массивов Y(3,6) и Х(5,4). 23 Вычислить количество единиц в матрицах А(5,5) и В(7,7). 24 Определить порядковые номера максимальных элементов массивов Z(10) и X(15). 25 Найти сумму наибольших элементов матриц C(9) и D(10). 26 Найти среднее арифметическое максимальных элементов, выбранных их двух векторов А(10) и В(12). 27 Даны целые числа n и m. Вычислить 28 Даны одномерные массивы С(12) и D(15). Вычислить 29 Вычислить значение функции 30 Найти произведение наименьших элементов матриц А(10) и D(15).
6.4.2 Использование подпрограммы-процедуры 1 Определить наименьшие элементы матриц А(5,4), В(5,3), а также номера строк и столбцов, в которых они находятся. 2 Найти максимальные элементы и их порядковые номера в массивах Х(10) и У(15). 3 Найти количество положительных, отрицательных и нулевых элементов для двух массивов А(3,5) и В(4,4). 4 Определить количество элементов в массивах А(12) и В(9), попадающих в интервал [-3, 5]. Элементы, попадающие в заданный интервал, запомнить в массивы А1 и В1 подряд. 5 Вычислить значение функции 6 Определить среднее арифметическое массивов А(10) и В(15) и количество элементов, меньших этого среднего. 7 Вычислить значение Amax и Bmax – максимальные элементы массивов А(15) и B(13). 8 Заданы три матрицы А(3,3), В(4,4), С(3,3). Найти минимальное из трех чисел Х, У, Z, которые являются следом матриц соответственно А, В, С. След матрицы - сумма элементов главной диагонали. 9 Даны матрицы А(3,3), С(7,7). Составить программу подсчета количества нулевых и отрицательных элементов матриц. 10 Найти количество элементов, значения которых попадают в интервал (1,5), и их сумму для массивов А(15), В(18). 11 Найти количество элементов, кратных 3, и сумму остальных элементов для целочисленных матриц А(3,3), В(3,4). 12 Найти произведение положительных и сумму отрицательных элементов для матриц В(3,5) и С(3,4). 13 Вычислить значение функции 14 Найти сумму положительных и количество отрицательных элементов для матриц В(5,3) и С(4,3). 15 Найти количество элементов, больших 5, меньших 5 и равных 5 для двух массивов А(3,5) и В(4,4). 16 Даны два массива D(5,5) и F(4,6), в каждом из них найти количество элементов со значениями в интервале (-5,5) и перемножить эти элементы. 17 Вычислить значение функции 18 Составить подпрограмму записи элементов прямоугольной матрицы в одномерный массив в порядке следования строк. Сделать это для матриц А(7,2) и В(5,3). 19 Найти сумму отрицательных и количество положительных элементов для матриц В(5,3) и С(4,3). 20 Найти количество элементов, кратных 5, и произведение остальных элементов для целочисленных матриц А(3,5), В(2,6). 21 Вычислить значение функции 22 Найти количество элементов, больших 1, меньших 1 и равных 1 для двух массивов С(3,5) и D(4,4). 23 Определить среднее арифметическое массивов А(4,4) и В(3,5) и количество элементов, больших этого среднего. 24 Найти сумму положительных и количество нулевых элементов для матриц X(5,5) и Y(4,6). 25 Вычислить значение функции 26 Вычислить значение где Xmin и Ymin – минимальные элементы массивов X(10) и Y(13). 27 Определить наибольшие элементы матриц А(5,5), В(6,6), а также номера строк и столбцов, в которых они находятся. 28 Найти математическое ожидание и дисперсию случайных величин, записанных в массивах Х(10) и Y(15). Вычисление производить в процедуре по формулам:
29 Вычислить значение где Amin и Bmin – минимальные элементы массивов А(15) и B(13); Amax и Bmax – максимальные элементы массивов А(15) и B(13). 30 Даны две квадратные вещественные матрицы порядка n. Определить в которой из них сумма максимальных элементов строк меньше.
6.5 Контрольные вопросы 1 Что такое подпрограмма? Для каких целей используются подпрограммы? 2 Чем отличаются подпрограмма-функция от подпрограммы-процедуры? 3 По каким правилам оформляются заголовки подпрограмм? 4 Как осуществляется вызов подпрограмм? 5 Каким образом объявляются в подпрограммах нестандартные типы данных, например, массивы? 6 В чем разница между фактическими (локальными) и формальными (глобальными) параметрами? 7 Что такое модуль? 8 Каким образом осуществляется обращение к модулю? 9 Опишите структуру модуля. 10 Перечислите стандартные модули и их назначение. Библиография
1 Симонович С.В. Информатика. Базовый курс.- СПб.: Питер, 2000. 2 ГОСТ 19.701-90. ЕСПД. Схемы алгоритмов и программ. Обозначения условные, графические. – М.: Издательство стандартов,1990. 3 С.Немнюгин, Л.Перколаб. Изучаем Turbo Pascal. – СПб.: Питер, 2001. О.А.Меженный.Turbo Pascal: учитесь программировать.- М.:Издательский дом «Вильямс», 2001. 5 Ю.Аляев, О.Козлов. Алгоритмизация и языки программирования Pascal, C++, Visual Basic: учебно-справочное пособие. – М.: Финансы и статистика, 2004.
|
, где А(n) и В(m)- одномерные массивы.
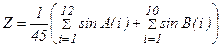, где А(12) и В(10) - заданные одномерные массивы.
, 
.
, где Xmax и Ymax - максимальные элементы массивов Х(10) и Y(15).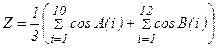
, где А(10) и В(12) - заданные одномерные массивы.
, 
, 
, T(15) и Q(15) - заданные массивы.
, где 
, 
.
. В подпрограмме вычисляется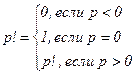 
.
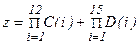, где Xmin и Ymin - минимальные элементы массивов Х(10) и Y(12).
, где x1, x2 – корни квадратного уравнения ax2+2x-5=0; y1, y2 – корни квадратного уравнения 7y2+ay-3=0.
, где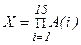 
, 
,
, где x1, x2 – корни квадратного уравнения ax2+bx+c=0; y1, y2 – корни квадратного уравнения dy2+ey+f=0.
, где 
, 
, Amax и Bmax – максимальные элементы массивов А(15) и B(13).
, где 
, 
, Amin и Bmin – минимальные элементы массивов А(12) и B(14).
, где 
,
, На рисунке 14 представлен второй вариант решения данной задачи, в котором вместо процедуры SUM введена вещественная функция SUM. Такая замена повлекла соответствующие изменения как в описании подпрограммы, так и в обращении к ней.
,
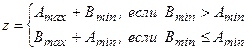