Программирование алгоритмов циклической структуры
Цель работы – ознакомление с особенностями программирования алгоритмов циклической структуры.
3.1 Алгоритмы циклической структуры. Операторы цикла Алгоритм, в котором предусмотрено многократное выполнение одной и той же последовательности действий, называется алгоритмом циклической структуры, а эта последовательность – циклом. Циклический алгоритм позволяет существенно сократить объем программы. Цикл можно организовать двумя способами: - с помощью счетчика и условия перехода (см. пример 2.2.1); - с помощью оператора цикла. В Паскале существует несколько операторов цикла. Оператор цикла представляет собой единую синтаксическую конструкцию, в которой можно выделить три основные части: заголовок цикла, тело цикла, заключительную строку. Заголовок цикла образуют ключевое слово и управляющая фраза, задающая способ управления повторениями. Заключительную строку составляет ключевое слово, заканчивающееся знаком “;”. Тело задает действия, которые повторяются в соответствии с правилами, заданными управляющей фразой. Если число повторений известно заранее (до начала повторений), то в такой ситуации лучше воспользоваться оператором цикла с параметром For-To или For-Downto (оператор цикла с фиксированным числом повторений). В остальных случаях следует использовать операторы цикла с предусловием While-Do или постусловием Repeat-Until. Оператор цикла с параметром имеет две модификации For-To и For-Downto и следующие ограничения: - i, m1, m2 могут быть только переменными целого типа; - параметр i не может изменяться внутри цикла. Все операторы цикла (For-To, For-Downto, While-Do и Repeat-Until) приведены в таблице D1. Общим для всех перечисленных операторов цикла является то, что циклы, организованные с их помощью, содержат обязательные компоненты: задание начального значения параметра цикла; тело цикла; задание шага изменения параметра цикла; проверку на выход из цикла. Для операторов While и Repeat изменение параметра цикла по какому-либо закону в теле цикла обязательно. При программировании алгоритмов циклической структуры часто используются приемы накапливания сумм, произведения, количества:
3.2 Примеры алгоритмов и программ циклической структуры 3.2.1 Вычислить все значения функции Y=A*K2, если К меняется от 1 до 10 с шагом 1. Решить задачу несколькими способами (на рисунках 3.1, 3.2, 3.3 и 3.4 показаны все способы решения задачи).
3.2.2 Вычислить значения функции Блок-схема и программа решения задачи представлены на рисунке 3.5.
При использовании оператора цикла For-To для решения данной задачи выбрать х в качестве параметра цикла нельзя, так как это вещественная переменная, кроме того, интервал ее изменения и шаг, также вещественные числа. Поэтому для организации цикла используем дополнительный параметр i, который будет изменяться параллельно с х требуемое число раз. Для этого определим количество итераций (повторений) по формуле:
3.3 Варианты заданий Решить задачу согласно варианту тремя способами, т.е. с использованием операторов цикла For-To (или For-Downto), While-Do и Repeat-Until. 1 Вычислить сумму четных и нечетных первых N чисел натурального ряда. 2 Дано целое число N. Вычислить P=N!=1´2´3´…´N. 3 Даны числа a и n. Вычислить P = a´(a-n) ´ (a-2n) ´ (a-3n) ´…´ (a-n2). 4 Вычислить произведение первых n сомножителей 5 Вычислить произведение четных и нечетных первых N чисел натурального ряда. 6 Даны вещественное число X и натуральное число n. Вычислить сумму первых n слагаемых S = sinX + sinX2 + sinX3 +…+ sinXn. 7 Даны вещественное число X и натуральное число n. Вычислить произведение первых N сомножителей S = sinX ´ sinX2 ´ sinX3 ´…´ sinXn. 8 Дано целое число n. Вычислить 9 Дано целое число n. Вычислить 10 Вычислить произведение первых n сомножителей 11 Даны вещественное число X и натуральное число n. Вычислить сумму первых n слагаемых 12 Даны вещественное число X и натуральное число n. Вычислить сумму первых n слагаемых 13 Даны числа b и n. Вычислить P = b´(b+1) ´ (b+2) ´ (b+3) ´…´ (b+n). 14 Вычислить сумму первых N чисел натурального ряда. 15 Вычислить произведение четных и нечетных первых N чисел натурального ряда. 16 Вычислить сумму первых n слагаемых 17 Дано целое число n. Вычислить 18 Даны числа x и n. Вычислить 19 Даны числа b и n. Вычислить P = (b-n) + (b - (n-1)) + (b- (n-2)) +…+ (b-1). 20 Даны вещественное число x и целое число n. Вычислить 21 Даны числа x и n. Вычислить 22 Дано целое число n. Вычислить 23 Дано целое число n. Вычислить 24 Дано целое число n. Вычислить 25 Дано целое число n. Вычислить 26 Дано целое число n. Вычислить 27 Даны числа a и n. Вычислить S = a+(a-n) + (a-2n) + (a-3n) +…+ (a-n2). 28 Даны вещественное число X и натуральное число n. Вычислить сумму первых n слагаемых S = sin2X + 2sin2X +…+ nsin2 X. 29 Дано целое число n. Вычислить 3.4 Контрольные вопросы 1 Что называется циклом? 2 Что представляет собой оператор цикла? 3 Какие виды оператора цикла существуют в Паскале? 4 Дайте сравнительную характеристику операторов For-To и For-Downto. 5 Что представляет собой оператор цикла While-Do? 6 Что представляет собой оператор цикла Repeat-Until? 7 Как организовать цикл For-To с вещественным параметром? 8 Как осуществляется накапливание суммы в программе? 9 Какое значение следует принять за начальное при накапливании произведения? 10 В какой последовательности выполняются действия при накапливании количества?
Приложение A Описание символов, используемых в графической схеме алгоритмов (ГСА)
Таблица А1 – Основные элементы блок-схем
Приложение В Основные элементы языка Турбо Паскаль Таблица В1 – Список зарезервированных слов
Таблица B2 – Перечень операций языка
Таблица В3 - Типы переменных (целые и действительные числа)
Приложение С Структура простейшей Паскаль-программы и встроенные функции языка Таблица С1 – Структура простейшей программы
Таблица С2 - Некоторые встроенные функции языка Паскаль
6.4 Обработка массивов
Цель работы – приобретение навыков программирования при решении задач с использованием одномерных и двумерных массивов, а также характерных приемов программирования.
4.1 Массивы и их обработка с помощью циклов Массив – это структурированный тип данных, состоящий фиксированного числа элементов одного типа. Массивы характеризуются именем, размерностью (количеством элементов), номерами (индексами) элементов в нем и значениями каждого элемента. Каждый элемент массива определяется своим индексом, по которому к нему осуществляется доступ. Одномерный массив иначе называется вектором. Элемент одномерного массива имеет один индекс, указывающий на его порядковый номер. Двумерный массив иначе называется матрицей. Элемент двумерного массива имеет два индекса: первый индекс соответствует номеру строки, второй – номеру столбца, в которых находится элемент. В таблице 4.1 приводятся характеристики вектора Х(4) и матрицы А(3,3). Таблица 4.1 - Примеры одномерного и двумерного массивов
Как и любой другой объект программы, массив должен быть объявлен. Существует два способа описания массива: - явный - в разделе Type описания типов данных (между Const и Var) задается размерность массива и тип его элементов, затем в разделе Var сформированному типу массива присваивается имя. Например,
- неявный - минуя раздел Type. Например,
Так в языке Паскаль нет возможности вводить и выводить массивы как единый объект, для обработки массивов используются операторы циклов. Ввод и вывод одномерных массивов возможен только поэлементно с помощью оператора цикла:
Работая с матрицей также надо организовать перебор всех ее элементов, причем необходимо открыть два цикла для изменения номера строки (i) и номера столбца (j), т.е. в одном цикле организовать другой. Таким образом, ввод и вывод двумерных массивов возможен только поэлементно с помощью организации вложенного цикла:
При таком способе организации вывода двумерный массив будет выведен на экране в одну строку. Если же в цикле использовать оператор Writeln (а[i,j]), то массив будет выведен в один столбец. Для того чтобы получить на экране матрицу в ее общепринятом виде, используется следующая организация вывода двумерного массива: For i:=1 to 4 do Begin For j:=1 to 5 do Write (а[i,j]); Writeln End; Пустой оператор Writeln в данном случае используется для перевода курсора на следующую строку. Циклы, аналогичные рассмотренному выше, называются вложенными. Цикл, в котором создается другой цикл, называется внешним, цикл, создаваемый внутри, - внутренним. Правила организации внешнего и внутреннего цикла те же, что и простого цикла. Вложенных циклов может быть больше двух. Параметры внешнего и внутреннего циклов должны быть разными, причем при фиксированном значении параметра внешнего цикла параметр внутреннего цикла принимает по очереди все свои значения. Как правило, характерные приемы программирования применяют к определенным элементам массивов, а именно: к элементам между заданными номерами строк и столбцов; при выполнении действий с элементами строк и столбцов; к элементам главной диагонали или параллельных ей; элементам побочной диагонали; элементам, расположенным выше и ниже главной диагонали. Для того чтобы алгоритм был составлен правильно, необходимо хорошо представлять взаимосвязь индексов элементов матрицы (таблица 4.2). Таблица 4.2 - Взаимосвязь индексов элементов матрицы
Если обработка массива идет построчно, то внешний цикл организуют по i, а внутренний по j, и, наоборот, при переборе элементов матрицы по столбцам внешний цикл организуют по j, а внутренний по i. Кроме того, если работа производится с элементами строк или столбцов, то между операторами открытия вложенных циклов или операторами их закрытия обычно стоит какой-либо оператор, осуществляющий действие со строкой или столбцом.
4.2 Примеры алгоритмов и программ обработки массивов 4.2.1 Найти наибольшее значение вектора Х(5) и его порядковый номер. На рисунке 4.1 представлены блок-схема алгоритма, программа и контрольная развертка. Алгоритм нахождения наибольшего элемента в векторе, рассматриваемый в этом примере, состоит в следующем: - задание некоторой промежуточной переменной значения равного значению одного из элементов массива; - организация цикла, в котором должен присутствовать условный оператор, сравнивающий значение очередного элемента массива и введенной переменной; - если элемент оказывается больше переменной, то ей присваивается значение этого элемента и при необходимости запоминается и его номер; - последнее значение переменной при выходе из цикла и будет наибольшим элементом массива.
4.2.2 Найти среднее арифметическое элементов вектора А(10). Блок-схема и программа решения задачи представлены на рисунке 4.2.
4.2.3 Найти количество положительных элементов матрицы А(4,5) среди элементов, расположенных выше главной диагонали. Блок-схема и программа решения задачи представлены на рисунке 4.3. При решении данной задачи перед открытием циклов, в которых будет осуществляться накапливание количества, необходимо обнулить начальное значение переменной К. Отбор элементов выполняется с использованием сложного условия, т.е. условие выбора положительных элементов массива и условие отбора элементов, расположенных выше главной диагонали, заключены в круглые скобки и объединены с помощью конъюнкции (аnd).
4.2.4 Найти количество положительных элементов каждой строки матрицы А(4,5). Блок-схема и программа решения задачи представлены на рисунке 4.4. В рассматриваемом примере обработка массива идет построчно, поэтому внешний цикл организуют по строкам (по индексу i), а внутренний по столбцам (по индексу j). Кроме того, между операторами открытия вложенных циклов стоит оператор, с помощью которого обнуляется начальное количество положительных элементов в каждой строке матрицы. Так как, открытый по строке цикл (по параметру i) содержит внутри себя несколько операторов, то для выделения их в единую последовательность, требуется применить операторные скобки Begin-End.
4.3 Варианты заданий 4.3.1 Характерные приемы программирования обработки одномерных массивов 1 Дано вещественное число А и массив Х(10). Определить номер элемента, равного А. Если такого члена нет, то ответом должен быть 0. 2 Вывести на печать первый отрицательный элемент массива Х(10) и его порядковый номер. 3 Переписать положительные элементы массива Y(10) подряд в массив Z. 4 Разделить последовательность А(10) на два массива, записать в один из них элементы с четными номерами, а в другой - с нечетными. 5 Вычислить сумму положительных элементов массива Z(10). 6 Для целочисленного массива Х(9) найти произведение его элементов с четными индексами и выяснить является ли оно нечетным числом. 7 Вычислить среднее арифметическое положительных элементов массива Y(10), имеющих нечетные индексы. Если таких элементов нет, то вывести на печать признак “0”. 8 Найти количество положительных чисел вещественного вектора Y(10). 9 Вычислить Z(j)=A(j)+B(j), где А(j)=j, если j- нечетные и А(j)=j/2, если j- четные; В(j)=j², если j- нечетные и В(j)=j³, если j - четные. 10 Для целочисленного массива Х(10) найти сумму его элементов, выяснить является ли результат четным числом. 11 Записать “1” вместо положительных элементов массива Х(12) и “0” - вместо отрицательных. 12 Дан массив Х(10). Все числа меньше 2 заменить “0” и вывести на печать их количество и порядковые номера. 13 Дан целочисленный массив А(10), получить последовательность В(10), которая отличается от исходной тем, что все нечетные элементы удвоены. 14 Найти произведение положительных элементов вектора А(15). 15 Вывести на экран отрицательные элементы массива Х(10). 16 Даны массивы А(10) и В(10). Получить вектор Z(10), где Z(j)=A(j)-B(j). 17 Вычислить произведение отрицательных элементов массива Z(10). 18 Записать в массив А(15) первые 5 элементов “0”, затем 5 элементов “2” и последние 5 - “3”. 19 Переписать массив А(10) в массив В(10) так, чтобы последний элемент стал первым, предпоследний - вторым и т.д. 20 Удвоить все элементы целочисленного вектора А(10), являющиеся четными числами и утроить все оставшиеся. 21 В массиве А(15) определить количество элементов, равных 5. 22 Найти количество нулевых элементов в массиве В(12). 23 Даны два вектора А(10) и В(10). Вычислить суммы и разности соответствующих элементов массивов. Результаты поместить в два вектора X(10) и Y(10). 24 В массиве C(13) определить количество элементов, равных 13. 25 В массиве X(11) определить количество элементов, меньших 5. 26 Вычислить сумму отрицательных элементов массива Z(10). 27 Вычислить произведение отрицательных элементов массива А(10). 28 Вычислить среднее арифметическое отрицательных элементов массива Y(10). 29 Найти количество неотрицательных элементов вектора В(12). 30 Даны два вектора А(10) и В(10). Вычислить произведение соответствующих элементов массивов. Результат поместить в вектор X(10).
4.3.2 Нахождение наибольшего (наименьшего) элемента в векторе 1 Найти наибольший отрицательный элемент среди элементов массива А(10), имеющих четные номера. 2 Найти наибольшее значение функции Z=Ax²+Bx+C в интервале изменения аргумента Х от 1 до 7 с шагом 0,5. Значения функции записать в массив Н. 3 Даны два массива Х(10) и Y(10). Найти среднее арифметическое i-ых элементов (i = 1,10) и записать их в массив Z. Среди элементов массива Z найти наибольший. 4 Найти наименьшее значение функции Y=sin(х2+5x)´cos(3x2-x) в интервале изменения аргумента x от 0 до 8 с шагом 0.4. Значение функции записать в массив А. 5 Найти наименьший положительный элемент среди элементов массива Х(10), имеющих нечетные номера. 6 Найти наибольшее значение Х(I)+Y(I) для массивов Х, Y. 7 Среди элементов массива А(10) найти наибольший. 8 Найти наименьший из положительных элементов массива А(10). 9 Найти наименьший положительный элемент среди элементов с четными номерами в массиве А(10). 10 Даны массивы A(5) и B(6). Найти суммы элементов в каждом массиве и запомнить их в массиве Z. Среди сумм определить наибольшую. 11 Даны массивы А(4) и С(6). Найти суммы положительных элементов каждого массива, запомнить их в массиве Х и найти среди них наименьшую. 12 Дан массив Х(20) и число А. среди элементов массива Х, расположенных до элемента А найти наибольший, а после него - наименьший. Если элемента А в массиве нет, выдать об этом сообщение. 13 Даны два одномерных массива А(10) и В(10). Получить массив С(10), элемент которого равен произведению соответствующих элементов массивов А и В. Среди элементов массива С найти наименьший. 14 В векторе Х(10) заменить нулем все отрицательные элементы, предшествующие его наибольшему элементу. 15 Среди четных номеров элементов массива В(10) найти наибольший. Элементы с нечетным номером обнулить. 16 В одномерном массиве С(20) просуммировать первый элемент с последним, второй с предпоследним и т.д. Результат записать в массив В(10) и в нем найти наибольший элемент. 17 Все элементы массива А(10), являющиеся четным числом, удвоить, а нечетным - возвести в квадрат. В полученном массиве найти наименьший элемент. 18 Из массива А(10) четные положительные числа записать в массив Х подряд. В новом массиве найти наименьший элемент. 19 Даны два одномерных массива. Найти суммы их элементов с четными номерами и среди сумм определить наибольшую. 20 Найти наименьший элемент среди элементов массива В(30), имеющих номера элементов кратные 3. 21 Среди элементов массива В(10) найти наименьший. 22 В массиве С(12) все элементы, стоящие до наибольшего обнулить. 23 В массиве С(9) все элементы, стоящие после наименьшего обнулить. 24 Найти наибольший среди элементов массива А(10), остальные обнулить. 25 Среди элементов массива В(10) найти наименьший положительный. 26 Наибольший элемент массива Х(12) удвоить, остальным элементам присвоить значение 1. 27 Поменять местами наибольший и наименьший элементы вектора А(10). 28 Все элементы массива А(10), являющиеся положительным числом, удвоить, а отрицательным - возвести в квадрат. В полученном массиве найти наименьший элемент. 29 Поменять местами наибольший отрицательный и наименьший положительный элементы вектора А(10). 30 Дан вектор Х(10). Найти количество элементов, стоящих после максимального по значению элемента.
4.3.3 Программирование алгоритмов работы с частями матрицы 1 Дана матрица А(5,5). Все элементы ниже главной диагонали обнулить, выше - заменить на“3”, а элементы главной диагонали заменить на “7”. 2 Найти произведение элементов главной диагонали матрицы Х(5,5). 3 Найти количество положительных элементов, расположенных ниже главной диагонали матрицы Y(5,5). 4 Переписать элементы главной диагонали матрицы В(5,5) в вектор X(5). 5 Вычислить произведение отрицательных элементов матрицы А(5,5), расположенных ниже главной диагонали. 6 Найти количество нулевых элементов матрицы В(4,4), расположенных выше главной диагонали. 7 Дана действительная квадратная матрица D(4,4). Заменить нулями все ее элементы, расположенные на главной диагонали и выше нее. 8 Вычислить среднее арифметическое элементов матрицы А(5,5), расположенных выше главной диагонали. 9 Вычислить среднее арифметическое элементов матрицы А(5,5), расположенных ниже главной диагонали. 10 Найти сумму элементов главной диагонали матрицы Х(5,5). 11 Найти произведение положительных элементов главной диагонали матрицы Х(5,5). 12 Найти произведение элементов побочной диагонали матрицы Х(6,6). 13 Найти сумму элементов побочной диагонали матрицы Х(5,5). 14 Переписать элементы побочной диагонали матрицы В(5,5) в вектор X(5). 15 Дана матрица А(5,5). Сформировать вектор из элементов, расположенных выше главной диагонали. 16 Дана матрица А(5,5). Сформировать вектор из элементов, расположенных ниже главной диагонали. 17 Дана матрица А(5,5). Найти максимальный по значению элемент среди элементов главной диагонали. 18 Вычислить сумму отрицательных элементов матрицы А(5,5), расположенных ниже главной диагонали. 19 Вычислить произведение положительных элементов матрицы Х(6,6), расположенных ниже главной диагонали. 20 Дана матрица В(5,5). Найти количество элементов, больших 5, среди элементов главной диагонали. 21 Дана матрица С(6,6). Найти количество элементов, меньших 5, среди элементов побочной диагонали. 22 Вычислить сумму положительных элементов матрицы Х(6,6), расположенных ниже главной диагонали. 23 Вычислить сумму положительных элементов матрицы А(5,5), расположенных выше главной диагонали. 24 Матрица А(5,5) делится на две части главной диагональю. Найти среднее геометрическое сумм элементов каждой части. 25 Матрица А(5,5) делится на две части побочной диагональю. Найти среднее арифметическое сумм элементов каждой части. 26 Вычислить сумму отрицательных элементов матрицы Х(6,6), расположенных выше главной диагонали. 27 Вычислить сумму отрицательных элементов матрицы А(5,5), расположенных выше главной диагонали. 28 Найти количество неотрицательных элементов главной диагонали матрицы Х(5,5). 29 Найти количество неотрицательных элементов побочной диагонали матрицы А(6,6). 30 Найти количество нулевых элементов матрицы В(4,4), расположенных ниже главной диагонали.
4.3.4 Программирование алгоритмов работы со строками и столбцами матрицы 1 Найти сумму элементов каждой строки матрицы А(5,5). Результат записать в вектор S(5). 2 Найти сумму элементов каждого столбца матрицы А(5,5). Результат записать в вектор S(5). 3 Найти количество отрицательных элементов каждого столбца матрицы Х(5,6). Результат записать в вектор К(6). 4 Найти количество положительных элементов каждого столбца матрицы В(5,6). Результат записать в вектор К(6). 5 Найти количество отрицательных элементов каждой строки матрицы Х(6,5). Результат записать в вектор К(6). 6 Дана матрица А(5,6). Найти сумму положительных элементов каждого четного столбца и произведение отрицательных элементов каждого нечетного столбца. 7 Найти среднее арифметическое элементов каждого столбца матрицы Х(3,4). Результат записать в вектор SA(4). 8 Найти среднее арифметическое элементов каждой строки матрицы Х(4,4). Результат записать в вектор SA(4). 9 Найти произведение элементов каждой строки матрицы А(5,5). Результат записать в вектор Р(5). 10 Найти произведение элементов каждого столбца матрицы А(5,5). Результат записать в вектор Р(5). 11 Дана матрица А(5,5) Найти такое К (1 £ К £ 5), чтобы элементы К-ой строки совпадали с элементами К-ого столбца. 12 Дана квадратная матрица порядка n. Исключить из нее строку и столбец, на пересечении которых расположен максимальный элемент главной диагонали. 13 Дана матрица С(7,7) в строках с отрицательным элементом на главной диагонали найти сумму всех элементов. Если на главной диагонали отрицательных элементов нет, то выдать об этом сообщение. 14 Найти произведение положительных элементов каждой строки матрицы А(6,5). Результат записать в вектор Р(6). 15 Найти произведение положительных элементов каждого столбца матрицы А(5,5). Результат записать в вектор Р(5). 16 Дана матрица С(6,6) в строках с положительным элементом на побочной диагонали найти сумму всех элементов. Если на побочной диагонали положительных элементов нет, то выдать об этом сообщение. 17 Дана матрица А(5,5) в столбцах с отрицательным элементом на главной диагонали найти сумму всех элементов. Если на главной диагонали отрицательных элементов нет, то выдать об этом сообщение. 18 Дана целочисленная матрица М(5,4), найти номера строк, все элементы которых равны. Если таких строк нет, то выдать об этом сообщение. 19 Дана квадратная матрица порядка n. Исключить из нее строку и столбец, на пересечении которых расположен минимальный элемент главной диагонали. 20 Найти среднее арифметическое положительных элементов каждого столбца матрицы Х(3,5). Результат записать в вектор SA(5). 21 Найти среднее арифметическое положительных элементов каждой строки матрицы Х(4,5). Результат записать в вектор SA(4). 22 Найти среднее арифметическое отрицательных элементов каждого столбца матрицы Х(3,4). Результат записать в вектор SA(4). 23 Найти среднее арифметическое отрицательных элементов каждой строки матрицы Х(4,4). Результат записать в вектор SA(4). 24 Найти количество неотрицательных элементов каждой строки матрицы Х(6,5). Результат записать в вектор К(6). 25 Найти среднее арифметическое неотрицательных элементов каждой строки матрицы А(5,5). Результат записать в вектор SA(5). 26 Дана матрица В(5,4), упорядочить элементы каждой строки матрицы по возрастанию. 27 Дана целочисленная матрица М(5,4), найти номера столбцов, все элементы которых равны. Если таких столбцов нет, то выдать об этом сообщение. 28 Дана матрица В(5,5), упорядочить элементы каждого столбца матрицы по возрастанию. 29 Найти количество нулевых элементов каждой строки матрицы Х(6,5). Результат записать в вектор К(6). 30 Найти количество нулевых элементов каждого столбца матрицы Х(5,6). Результат записать в вектор К(6).
4.4 Контрольные вопросы 1 Что такое «массив»? 2 Чем характеризуются элементы массива? 3 Чем отличаются явный и неявный способы объявления массивов? 4 Какие способы ввода массивов существуют в Паскале? 5 Чем отличается вывод элементов массива в строку и в столбец? 6 Какие действия необходимо выполнить для подсчета суммы элементов одномерного массива? 7 Что изменится в алгоритме при подсчете количества отрицательных элементов в массиве? 8 Как выполнить поиск наибольшего (наименьшего) элемента в массиве? 9 Каковы особенности работы с квадратной матрицей? 10 Как организовать обработку матрицы по столбцам (по строкам)?
|




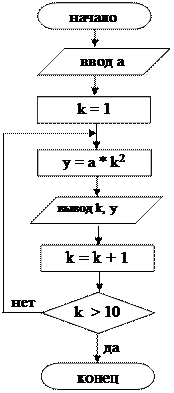
 для х, меняющегося в интервале от –5 до 7 с шагом 0,5. Найти количество (К) значений у(х) равных нулю, сумму (S) положительных значений у(х) и произведение (P) отрицательных значений у(х). Решить задачу, используя, оператор For-To.
для х, меняющегося в интервале от –5 до 7 с шагом 0,5. Найти количество (К) значений у(х) равных нулю, сумму (S) положительных значений у(х) и произведение (P) отрицательных значений у(х). Решить задачу, используя, оператор For-To.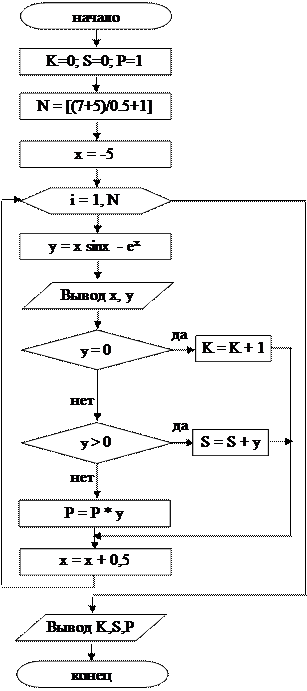
 , где m1 и m2 - начальное и конечное значение х, m3 – шаг. Так как значение N не всегда получается целым числом, в программе рекомендуется использовать функцию trunc(x), результатом которой является целое число, а аргументом - вещественное. Вычисления значения функции производятся в цикле. До организации цикла необходимо задать начальные значения переменных для хранения суммы (S=0), количества (K=0) и произведения (P=1). Также необходимо задать начальное значение переменной (х =-5), а затем внутри цикла изменять х на величину шага (х:= х + 0.5). Для накопления суммы и количества в теле цикла используется оператор присваивания типа счетчика, суть которого: последующее значение = предыдущее значение + текущее значение (S:= S + y и K:= K +1), а для накопления произведения используется идентичный оператор присваивания, но со знаком * в правой его части (P:= P * y).
, где m1 и m2 - начальное и конечное значение х, m3 – шаг. Так как значение N не всегда получается целым числом, в программе рекомендуется использовать функцию trunc(x), результатом которой является целое число, а аргументом - вещественное. Вычисления значения функции производятся в цикле. До организации цикла необходимо задать начальные значения переменных для хранения суммы (S=0), количества (K=0) и произведения (P=1). Также необходимо задать начальное значение переменной (х =-5), а затем внутри цикла изменять х на величину шага (х:= х + 0.5). Для накопления суммы и количества в теле цикла используется оператор присваивания типа счетчика, суть которого: последующее значение = предыдущее значение + текущее значение (S:= S + y и K:= K +1), а для накопления произведения используется идентичный оператор присваивания, но со знаком * в правой его части (P:= P * y). .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.








 - абсолютное значение величины х
- абсолютное значение величины х
 , x>=0
, x>=0

 т.е. а 23 = 0; а 32 = 4.2
т.е. а 23 = 0; а 32 = 4.2







