Первый множитель в (6) обращается в нуль в точках, для которых
В этих точках интенсивность, создаваемая каждой из щелей в отдельности, равна нулю (см. условие (2)). Второй множитель в (6) принимает значение
Для направлений, определяемых этим условием, колебания от отдельных щелей взаимно усиливают друг друга, вследствие чего амплитуда колебаний в соответствующей точке экрана равна
( Условие (8) определяет положения максимумов интенсивности, называемых главными. Число Возведя равенство (9) в квадрат, получим, что интенсивность главных максимумов Кроме минимумов, определяемых условием (7), в промежутках между соседними главными максимумами имеется
В формуле (10) Условие (10) легко получить методом графического сложения колебаний. Колебания от отдельных щелей изображаются векторами одинаковой длины. Согласно (10) каждый из последующих векторов повернут относительно предыдущего на один и тот же угол
Поэтому в тех случаях, когда Между дополнительными минимумами располагаются слабые вторичные максимумы. Число таких максимумов, приходящееся на промежуток между соседними главными максимумами, равно На рис. 8 приведен график функции (6) для
максимум Количество наблюдающихся главных максимумов определяется отношением периода решетки Определим угловую ширину центрального (нулевого) максимума. Положение ближайших к нему дополнительных минимумов определяется условием
Положение дополнительных минимумов, ближайших к главному максимуму
Обозначив
При большом числе щелей значение
При
Произведение В дифракционном спектре положение главных максимумов зависит от длины волны Основными характеристиками всякого спектрального прибора являются его дисперсия и разрешающая сила. Дисперсия определяет угловое или линейное расстояние между двумя спектральными линиями, отличающимися по длине волны на единицу (например, на Угловой дисперсией называется величина
где Чтобы найти угловую дисперсию дифракционной решетки, продифференцируем условие (8) главного максимума слева по
Отсюда
В пределах небольших углов
– угловая дисперсия обратно пропорциональна периоду решетки Линейной дисперсией называют величину
Приняв во внимание выражение (11), получим для линейной дисперсии дифракционной решетки (при небольших
Разрешающей силой спектрального прибора называют безразмерную величину
где Возможность разрешения (т. е. раздельного восприятия) двух близких спектральных линий зависит не только от расстояний между ними (которое определяется дисперсией прибора), но также и от ширины спектрального максимума. На рис. 10 показана результирующая интенсивность (сплошные кривые), наблюдающаяся при наложении двух близких максимумов (пунктирные кривые). В случае а) оба максимума воспринимаются как один. В случае б) между максимумами лежит минимум. Два близких максимума воспринимаются глазом раздельно в том случае, если интенсивность в промежутке между ними составляет не более 80% от интенсивности максимума. Согласно критерию, предложенному Рэлеем, такое соотношение интенсивностей имеет место в том случае, если середина одного максимума совпадает с краем другого (рис. 10. б). Такое взаимное расположение максимумов получается при определенном (для данного прибора) значении Найдем разрешающую силу дифракционной решетки. Положение середины
Края
Середина максимума для длины волны
Решив это соотношение относительно Таким образом, разрешающая сила дифракционной решетки пропорциональна порядку спектра
2. ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ Прибор гониометр Г-5 смонтирован на массивном металлическом основании. Его оптическая система (см. рис.11) состоит из коллиматора 1, обеспечивающего получение параллельного пучка света, зрительной трубы 2, и отсчетного микрометра 3 и ряда других узлов, смонтированных внутри корпуса прибора. Установка включает в себя также источник света – осветитель 4. На предметном столике 5, который может вращаться вокруг вертикальной оси, в специальном крепежном узле установлена дифракционная решетка с периодом Электрическая цепь прибора предполагает питание части узлов непосредственно от электрической сети, а части узлов – через понижающий трансформатор. Трансформатор имеет регулятор напряжения, позволяющий регулировать накал лампы осветителя. Желательно накал лампы устанавливать не предельный, а несколько ниже, чтобы не допускать перегрева корпуса. Питание измерительной оптической линии включается с помощью тумблера 10 на левой стороне корпуса прибора (внизу), а питание осветительного блока 4 с помощью тумблера 11 на корпусе трансформатора.
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Включить осветитель 4. Поставить зрительную трубку таким образом, чтоб в центре поля зрения было четко видно изображение входной щели коллиматора (максимум нулевого порядка). В этом положении продольные оси осветителя, коллиматора и зрительной трубы должны располагаться по одной прямой. Дифракционная решетка закреплена так, чтобыее плоскость была перпендикулярна этой прямой. 2. Тумблером 11, расположенным на левой стороне корпуса внизу, включить освещение отсчетного устройства. Через окуляр отсчетного микрометра 3 прочитать показания: верхняя шкала – 0º, нижняя шкала – 180º. Следовательно, прибор настроен, можно приступать к дальнейшей работе. Если настройка прибора сбита, обратиться к лаборанту или преподавателю. 3. Медленно поворачивая зрительную трубу влево (действие прикладывается к корпусу алидады), наблюдать спектр первого порядка.При этом вертикальная нить поля зрительной трубы совмещается с фиолетовым участком спектра (ближе к его левому краю). 4. Произвести отсчет угла, соответствующего положению максимума фиолетового участка спектра первого порядка ПРИМЕЧАНИЕ. Если запаса хода маховичка не хватает, следует немного сдвинуть зрительную трубу гониометра и сделать такое совпадение возможным. Число градусов равно ближайшей левой цифре от вертикального индекса, находящегося несколько выше шкалы. Число десятков минут равно числу интервалов, заключенных между верхним штрихом, который соответствует отсчитанному числу градусов, и нижним оцифрованным штрихом, отличающимся от верхнего на 180º. Вести отсчеты с большей точностью не имеет смысла, т.к. значительны погрешности других сопутствующих операций.
На рис.12 показание прибора 22º30¢: ближайшая цифра от метки слева 22, и от цифры 22 по нижней шкале до цифры 22+180=202 три деления, это дает нам десятки минут. Итак, имеем 22º30¢. Навести вертикальную нить зрительной трубы на красный участок спектра первого порядка (ближе к краю спектра) и сделать отсчет 5. Перемещая трубу далее влево, наблюдать спектр второго порядка. Аналогично произвести измерения
6. Возвратить зрительную трубу в положение На рис.12 показание прибора: 357º40¢, значение угла 7. Повторить измерения таким образом, чтобы сформировалась статистика из 8 результатов для фиолетового и 8 результатов для красного участка спектра. Данные наблюдений занести в таблицу. (Совпадающие значения Таблица 1
8. Поворачивая зрительную трубу влево и вправо, установить максимальный порядок наблюдаемого спектра
4. ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА Обработка результатов экспериментов включает в себя получение наиболее вероятных значений границ белого света и анализ полученных результатов. Анализ предполагает получение значений выборочной дисперсии и значений доверительных интервалов при заданном уровне вероятности. Для выполнения этой части работы рекомендуется обратиться к учебному пособию «Вопросы математической организации физического эксперимента».
где
5. ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ ОТЧЕТА Отчет к лабораторной работе должен включать в себя формулировку цели работы, перечень приборов и оборудования и их характеристики, принципиальную схему лабораторной установки, расчетные формулы, таблицу результатов экспериментов, расчет разрешающей способности и угловой дисперсии решетки, выводы по работе.
6. КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ 1. В чем состоит принцип Гюйгенса? Какие дополнения внес в этот принцип Френель? 2. В чем состоит явление дифракции света? 3. Как рассчитать амплитуду колебаний, возникающих в результате дифракции в параллельных лучах от щели? 4. Получите условия максимумов и минимумов интенсивности при дифракции от щели. 5. Получите зависимость интенсивности I от угла дифракции 6. Чем определяется количество минимумов интенсивности при дифракции от щели? 7. Решите задачу о дифракции Фраунгофера от щели методом графического сложения амплитуд. 8. Выведите формулу для интенсивности света, создаваемой дифракционной решеткой при угле дифракции 9. Получите условия добавочных минимумов, создаваемых дифракционной решеткой, методом графического сложения колебаний. 10. Определите угловую ширину 11. Что такое угловая дисперсия? Получите выражение для угловой дисперсии дифракционной решетки. 12. Как определить разрешающую силу дифракционной решетки?
7. ЛИТЕРАТУРА 1. Савельев, И.В. Курс общей физики. В 3-х т. [Текст]: Учебное пособие / И. В. Савельев. – Изд.5-е, стереотип. – СПб.: Изд-во “Лань”, 2006. – 486с. – Т. 2. – с. 381–415- (Электричество и магнетизм. Волны. Оптика). 2. Иродов И.Е. Волновая механика. Основные законы [Текст]/ И.Е.Иродов.– М.: Лаборатория Базовых Знаний, 2001–256 с.
|


 . (7)
. (7) в точках, удовлетворяющих условию
в точках, удовлетворяющих условию ,
,  . (8)
. (8) (9)
(9) – амплитуда колебания, посылаемого одной щелью под углом
– амплитуда колебания, посылаемого одной щелью под углом  ).
). дает порядок главного максимума. Максимум нулевого порядка только один, максимумов 1-го, 2-го и т. д. порядков имеется по два.
дает порядок главного максимума. Максимум нулевого порядка только один, максимумов 1-го, 2-го и т. д. порядков имеется по два. в
в  раз больше интенсивности
раз больше интенсивности  , создаваемой в направлении
, создаваемой в направлении  .
. добавочных минимумов. Эти минимумы возникают в тех направлениях, для которых колебания от отдельных щелей взаимно погашают друг друга. Направления добавочных минимумов определяются условием
добавочных минимумов. Эти минимумы возникают в тех направлениях, для которых колебания от отдельных щелей взаимно погашают друг друга. Направления добавочных минимумов определяются условием , (10)
, (10) .
. Рис. 7
Рис. 7
 принимает все целочисленные значения, кроме
принимает все целочисленные значения, кроме 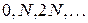 , т. е. кроме тех, при которых условие (10) переходит в (8).
, т. е. кроме тех, при которых условие (10) переходит в (8). .
. , мы, пристраивая начало следующего вектора к концу предыдущего, получим замкнутую ломаную линию, которая делает
, мы, пристраивая начало следующего вектора к концу предыдущего, получим замкнутую ломаную линию, которая делает  ) или
) или 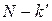 (при
(при  ) оборотов прежде, чем конец
) оборотов прежде, чем конец  и значений
и значений 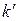 , равных
, равных  и
и  .
. 
 . Ранее было показано, что интенсивность вторичных максимумов не превышает
. Ранее было показано, что интенсивность вторичных максимумов не превышает  интенсивности ближайшего главного максимума.
интенсивности ближайшего главного максимума. и
и  . Пунктирная кривая, проходящая через вершины главных максимумов, изображает интенсивность от одной щели, умноженную на
. Пунктирная кривая, проходящая через вершины главных максимумов, изображает интенсивность от одной щели, умноженную на  главные максимумы 3-го, 6-го и т. д. порядков приходятся на минимумы интенсивности от одной щели, вследствие чего эти максимумы пропадают. Вообще из формул (7) и (8) вытекает, что главный максимум
главные максимумы 3-го, 6-го и т. д. порядков приходятся на минимумы интенсивности от одной щели, вследствие чего эти максимумы пропадают. Вообще из формул (7) и (8) вытекает, что главный максимум  -й минимум от одной щели, если будет выполнено равенство:
-й минимум от одной щели, если будет выполнено равенство:  , или
, или  . Это возможно, если
. Это возможно, если  равно отношению двух целых чисел
равно отношению двух целых чисел  и
и  (практический интерес представляет случай, когда эти числа невелики). Тогда главный
(практический интерес представляет случай, когда эти числа невелики). Тогда главный Рис. 8
Рис. 8
 -го порядка - на
-го порядка - на  -й минимум и т. д., в результате чего максимумы порядков
-й минимум и т. д., в результате чего максимумы порядков  и т. д. будут отсутствовать.
и т. д. будут отсутствовать. к длине волны
к длине волны 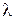 . Модуль
. Модуль  не может превысить единицу. Поэтому из формулы (8) вытекает что
не может превысить единицу. Поэтому из формулы (8) вытекает что  .
. (см. формулу (10)), этим минимумам соответствуют
(см. формулу (10)), этим минимумам соответствуют  , где
, где  ,
,  .
. Рис. 9
Рис. 9
 . Отсюда получается для угловой ширины
. Отсюда получается для угловой ширины  .
. и
и  , имеем
, имеем .
. будет очень мало, потому
будет очень мало, потому  , и
, и .
.

 Рис. 10
Рис. 10
 дает длину дифракционной решетки. Следовательно, угловая ширина главных максимумов обратно пропорциональна длине решетки. С увеличением порядка максимума
дает длину дифракционной решетки. Следовательно, угловая ширина главных максимумов обратно пропорциональна длине решетки. С увеличением порядка максимума  возрастает.
возрастает. ). Разрешающая сила определяет минимальную разность длин волн
). Разрешающая сила определяет минимальную разность длин волн  , при которой две линии воспринимаются в спектре раздельно.
, при которой две линии воспринимаются в спектре раздельно. ,
, – угловое расстояние между спектральными линиями, отличающимися по длине волны на
– угловое расстояние между спектральными линиями, отличающимися по длине волны на  .
. .
. , поэтому можно положить
, поэтому можно положить (11)
(11) , где
, где 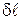 – линейное расстояние на экране или на фотопластинке между спектральными линиями, отличающимися по длине волны на
– линейное расстояние на экране или на фотопластинке между спектральными линиями, отличающимися по длине волны на  , где
, где  – фокусное расстояние линзы, собирающей дифрагирующие лучи на экране. Следовательно, линейная дисперсия связана с угловой дисперсией
– фокусное расстояние линзы, собирающей дифрагирующие лучи на экране. Следовательно, линейная дисперсия связана с угловой дисперсией  соотношением
соотношением .
. .
. ,
, определяется условием
определяется условием .
. .
. . Отсюда
. Отсюда .
. , получим выражение для разрешающей силы
, получим выражение для разрешающей силы  .
. м. Решетка установлена перпендикулярно световому потоку, выходящему из коллиматора. Фиксация установки дифракционной решетки производится с помощью винтов 6 и 7, эта операция выполняется лаборантом при подготовке прибора к работе. Непосредственно под предметным столиком расположен крупногабаритный узел 8, называемый алидадой. Внутри ее корпуса находится отсчетный лимб (круглая шкала). Показания прибора снимаются с помощью отсчетного микрометра 3.
м. Решетка установлена перпендикулярно световому потоку, выходящему из коллиматора. Фиксация установки дифракционной решетки производится с помощью винтов 6 и 7, эта операция выполняется лаборантом при подготовке прибора к работе. Непосредственно под предметным столиком расположен крупногабаритный узел 8, называемый алидадой. Внутри ее корпуса находится отсчетный лимб (круглая шкала). Показания прибора снимаются с помощью отсчетного микрометра 3.
 Общий вид прибора-гониометра Г-5
Рис.11
1 – коллиматор; 2 – зрительная труба; 3 – отсчетный микроскоп; 4 – осветитель;
5 – предметный столик; 6, 7 – фиксирующие винты; 8 – алидада; 9 – корпус основания;
12 – маховичок оптического микрометра. Включение освещения измерительной линии прибора – тумблер на корпусе основания с левой стороны.
Общий вид прибора-гониометра Г-5
Рис.11
1 – коллиматор; 2 – зрительная труба; 3 – отсчетный микроскоп; 4 – осветитель;
5 – предметный столик; 6, 7 – фиксирующие винты; 8 – алидада; 9 – корпус основания;
12 – маховичок оптического микрометра. Включение освещения измерительной линии прибора – тумблер на корпусе основания с левой стороны.
 (1). Отсчет производить через микроскоп 3. Чтобы снять отсчет, нужно, глядя в окуляр отсчетного микроскопа 3, повернуть маховичок 12 оптического микрометра так, чтобы верхние и нижние изображения штрихов лимба точно совпадали.
(1). Отсчет производить через микроскоп 3. Чтобы снять отсчет, нужно, глядя в окуляр отсчетного микроскопа 3, повернуть маховичок 12 оптического микрометра так, чтобы верхние и нижние изображения штрихов лимба точно совпадали. Рис. 12. Пример отсчета показания прибора
Рис. 12. Пример отсчета показания прибора
 (1).
(1). (2) и
(2) и  Рис. 13. Пример отсчета показания прибора при правом положении зрительной трубы
Рис. 13. Пример отсчета показания прибора при правом положении зрительной трубы
 . Линейкой измерить ширину решетки
. Линейкой измерить ширину решетки  . Вычислить разрешающую способность решетки
. Вычислить разрешающую способность решетки  и угловую дисперсию
и угловую дисперсию  .
. ,
,  ,
,  ,
,  ,
, ,
,  – результаты
– результаты  -го измерения.
-го измерения. ,
,  .
.


