Таблица 1 – Приближённые значения удельных сопротивлений грунтов
| Грунт
| Удельное сопротивление,
R·10, Ом·м
| Грунт
| Удельное сопротивление,
R·10, Ом·м
|
| Возможные пределы колебаний
| При влажности 10-12% к массе грунта
| Возможные пределы колебаний
| При влажности 10-12% к массе грунта
|
| Песок
| 40 - 90
|
| Чернозем
| 9 - 200
|
|
| Супесок
| 15 - 40
|
| Речная вода
| 5,0
| -
|
| Суглинок
| 0,4 - 15
|
| Морская вода
| 0,002 - 0,01
| -
|
| Глина
| 0,8 - 7
|
|
|
|
|
Таблица 2 – Значения повышающего коэффициента К
| Заземлитель
| К в зависимости от климатической зоны
|
| Ι
| ΙΙ
| ΙΙΙ
| ΙV
|
| Протяженный заземлитель на глубине 0,8 м
| 4,5-7
| 3,5-4,5
| 2-2,5
| 1,5-2
|
| Стержневой заземлитель длиной 2,5 - 3 м при расстоянии от поверхности земли до заземлителя 0,8 м
| 1,8-2
| 1,6-1,8
| 1,4-1,6
| 1,2-1,4
|
| Примерное расположение республик и областей
| Карелия
| Ленинградская область
| Латвия
| Молдавия
|
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Состояние электрона в атоме определяется волновой функцией 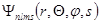 , аналитическое выражение которой зависит от квантовых чисел
, аналитическое выражение которой зависит от квантовых чисел  . Для нерелятивистского случая волновая функция
. Для нерелятивистского случая волновая функция  находится из решения уравнения Шредингера:
находится из решения уравнения Шредингера: 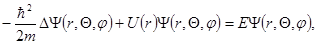
где ħ – постоянная Планка, m – масса электрона, Δ- оператор Лапласа, E – энергия электрона.
Задача нахождения волновой функции  решается точно только для атома водорода, для других атомов (многоэлектронных)
решается точно только для атома водорода, для других атомов (многоэлектронных)  находят, с использованием приближенных методов (например, метода Хартри-Фока).
находят, с использованием приближенных методов (например, метода Хартри-Фока).
В атоме водорода электрон движется в электрическом поле ядра с потенциалом  , где
, где  - заряд ядра, Z – порядковый номер элемента (для водорода Z= 1).
- заряд ядра, Z – порядковый номер элемента (для водорода Z= 1).
При решении уравнения Шредингера необходимо учитывать сферическую симметрию электрического поля и явную независимость r от t, тогда волновую функцию уравнения представляют как произведение трех функций 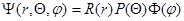 .
.
Решая уравнение Шредингера с  , методом разделения переменных, получим выражение для R(r), P(Θ), Φ(φ) и значение
, методом разделения переменных, получим выражение для R(r), P(Θ), Φ(φ) и значение 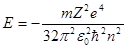 ;
;
 (полином Лаггера), где n =1, 2, 3,…∞;
(полином Лаггера), где n =1, 2, 3,…∞;
 - безразмерный параметр;
- безразмерный параметр; 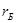 - радиус Бора (наименьшее расстояние электрона от ядра в атоме водорода).
- радиус Бора (наименьшее расстояние электрона от ядра в атоме водорода).
 (полином Лежандра).
(полином Лежандра).
 - определяют из условия нормировки
- определяют из условия нормировки  .
.
Из полученных результатов следует, что энергия электрона в атоме зависит от квантового числа n, аналитическое выражение для R(r) зависит от чисел n и l, а P(Θ) –от ml и l. Таким образом волновая функция, описывающая состояние электрона в атоме водорода  , равна произведению полинома Лаггера, полинома Лежандра и
, равна произведению полинома Лаггера, полинома Лежандра и  .
.
Например: для Z= 1, n= 2, l= 0
 ;
;
для Z= 1, n= 1, l= 0
 .
.
Для полинома Лежандра получим (n= 2, l= 1, m= 0 и n= 2, l= 1, m= 1):
 ; и соответственно
; и соответственно
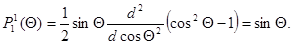
Электронная плотность 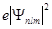 (или электронное облако, орбиталь, облако вероятности) будет иметь вид:
(или электронное облако, орбиталь, облако вероятности) будет иметь вид:

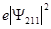
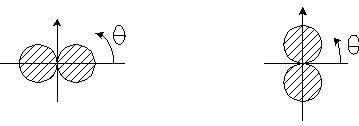
для n= 2, l= 1, m= 0 для n= 2, l= 1, m= 1
Квантовое число S появляется при решении уравнения Дирака,описывающего состояние электрона в атоме водорода в релятивистском приближении.
Физический смысл квантовых чисел заключается в следующем: квантовое число  - определяет энергию электрона в атоме; квантовое число
- определяет энергию электрона в атоме; квантовое число  - определяет величину орбитального углового момента электрона
- определяет величину орбитального углового момента электрона 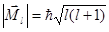 и форму электронного облака; а
и форму электронного облака; а 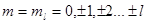 - проекцию этого углового момента на избранную ось (Z)
- проекцию этого углового момента на избранную ось (Z)  ; квантовое число
; квантовое число  - определяет собственный угловой момент электрона (спин)
- определяет собственный угловой момент электрона (спин)  ; а
; а 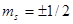 - проекцию спина на избранную ось (Z)
- проекцию спина на избранную ось (Z)  . Количество проекций орбитального углового момента электрона равно 2 l +1; спинового - 2 s +1.
. Количество проекций орбитального углового момента электрона равно 2 l +1; спинового - 2 s +1.
В многоэлектронном атоме угловые моменты складываются по правилу параллелограмма с учетом их дискретного изменения. Сложение угловых моментов происходит различным образом для «тяжелых» и «легких» атомов.
Для «легких» атомов механизм сложения определен Расселом и Саундерсом. Он состоит в том, что отдельно складываются орбитальные угловые моменты электронов  , образуя полный орбитальный момент атома
, образуя полный орбитальный момент атома  , величина которого определяется квантовым числом L:
, величина которого определяется квантовым числом L: 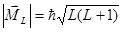 ,
,
где для двух электронов 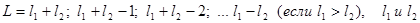 - квантовые числа орбитального углового момента первого и второго электронов. Проекция полного углового орбитального момента атома на ось Z определяется квантовым числом
- квантовые числа орбитального углового момента первого и второго электронов. Проекция полного углового орбитального момента атома на ось Z определяется квантовым числом  :
:  , где
, где  , число проекций полного углового орбитального момента атома равно
, число проекций полного углового орбитального момента атома равно  .
.
Отдельно складываются собственные угловые моменты электронов  , т.к.
, т.к.  , а
, а  , то квантовое число полного собственного углового момента S будет равно сумме всех
, то квантовое число полного собственного углового момента S будет равно сумме всех  с учетом их знаков. Величина собственного полного углового момента атома равна
с учетом их знаков. Величина собственного полного углового момента атома равна  .
.
Полный угловой момент атома  , равный векторной сумме
, равный векторной сумме  и
и  , определяется квантовым числом J,
, определяется квантовым числом J,
 , где
, где  , если
, если 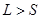 .
.
Для «тяжелых» атомов механизм сложения угловых моментов иной: складываются собственный и орбитальный моменты отдельного электрона:  . Полные угловые моменты электронов
. Полные угловые моменты электронов  , складываясь векторно, дают полный угловой момент атома
, складываясь векторно, дают полный угловой момент атома  ,
,  где
где  , если
, если  .
.
Кроме механических угловых моментов атом имеет и соответствующие магнитные моменты, зависящие от механических угловых моментов атома:
 где
где  (1)
(1)
β; - магнетон Бора;  - гиромагнитное отношение:
- гиромагнитное отношение:  ;
;  - фактор Ланде, значения которого для свободного атома равно:
- фактор Ланде, значения которого для свободного атома равно: 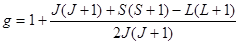 ; (2) m0 – масса покоя электрона.
; (2) m0 – масса покоя электрона.
Фактор Ланде связан с неколлениарностью векторов  и
и  , обусловленной разным значением гиромагнитных отношений орбитального и спинового моментов:
, обусловленной разным значением гиромагнитных отношений орбитального и спинового моментов: 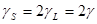 .
.
Распределение электронов атома по энергиям (энергетическим уровням) определяется принципом Паули и минимальным значением энергии атома, заполнение уровней начинается с уровня  , имеющего минимальную энергию.
, имеющего минимальную энергию.
Согласно принципу Паули, в атоме не существует двух и более электронов с одинаковыми четырьмя квантовыми числами  (с учетом того, что
(с учетом того, что  может принимать значения ±1/2). Задавая определенное значение квантового числа
может принимать значения ±1/2). Задавая определенное значение квантового числа  , мы тем самым задаем значения квантовых чисел
, мы тем самым задаем значения квантовых чисел  и
и  . Все электроны, имеющие одинаковое квантовое число
. Все электроны, имеющие одинаковое квантовое число  , образуют оболочку. Оболочкам даны такие обозначения: K-оболочка (n=1); L-оболочка (n=2); M-оболочка (n=3) и т.д. Электроны с одинаковыми квантовыми числами
, образуют оболочку. Оболочкам даны такие обозначения: K-оболочка (n=1); L-оболочка (n=2); M-оболочка (n=3) и т.д. Электроны с одинаковыми квантовыми числами  образуют подоболочку. Подоболочки обозначаются так:
образуют подоболочку. Подоболочки обозначаются так:  -подоболочка (
-подоболочка ( =0); p-подоболочка (
=0); p-подоболочка ( =1); d-подоболочка (
=1); d-подоболочка ( =2); f-подоболочка (
=2); f-подоболочка ( =3) и т.д.
=3) и т.д.
Энергетические уровни электрона обозначают символом, называемым энергетическим термом 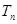 , разность двух энергетических термов определяет частоту излучаемого фотона
, разность двух энергетических термов определяет частоту излучаемого фотона 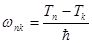 .
.
Для данного значения n, квантовые числа атома  могут принимать различные значения. Символ, содержащий информацию о квантовых числах
могут принимать различные значения. Символ, содержащий информацию о квантовых числах  , называют спектральным термом. Для
, называют спектральным термом. Для  термы обозначают буквами
термы обозначают буквами  соответственно, вверху слева от буквы, обозначающей терм, пишется число, равное
соответственно, вверху слева от буквы, обозначающей терм, пишется число, равное  , называемое мультиплетностью терма, внизу справа – квантовое число J, например
, называемое мультиплетностью терма, внизу справа – квантовое число J, например  (для этого спектрального терма:
(для этого спектрального терма:  ).
).
Величина магнитного момента атома (иона) зависит от количества электронов атома, находящихся на не полностью заполненной подоболочке атома. Заметим, что в силу принципа Паули, магнитный момент электронов полностью заполненной подоболочки равен нулю (в этом случае S=L=J= 0).
При комнатной температуре и отсутствии внешнего воздействия на атом он будет находиться в основном состоянии, которое характеризуется минимумом энергии ( ). Спектральный терм основного состояния находится по правилам Хунда, с учетом принципа Паули: минимальную энергию имеет атом, если его спиновое число
). Спектральный терм основного состояния находится по правилам Хунда, с учетом принципа Паули: минимальную энергию имеет атом, если его спиновое число  имеет максимальное значение, и при
имеет максимальное значение, и при  максимальным должно быть орбитальное квантовое число
максимальным должно быть орбитальное квантовое число  . Определив
. Определив  и
и  , можно найти квантовое число
, можно найти квантовое число  полного углового момента атома:
полного углового момента атома:  , где «+» берут, если число электронов на подоболочке больше половины, и «-», если меньше половины. Для подоболочки, заполненной наполовину
, где «+» берут, если число электронов на подоболочке больше половины, и «-», если меньше половины. Для подоболочки, заполненной наполовину  , и тогда
, и тогда  . Число электронов на подоболочке равно:
. Число электронов на подоболочке равно:  .
.
Для атомов (ионов) с подоболочкой, заполненной менее, чем наполовину  , где
, где  - число нескомпенсированных электронов на подоболочке. Для подоболочки с квантовым числом
- число нескомпенсированных электронов на подоболочке. Для подоболочки с квантовым числом  , заполненной более чем наполовину
, заполненной более чем наполовину  , например, для ионов 3dа S=1/2(10-а).
, например, для ионов 3dа S=1/2(10-а).
В данной работе измеряются магнитные моменты ионов атомов группы 3dа (группа железа). Ионы входят в состав твердого тела, поэтому они не являются свободными, а находятся в электрическом поле, создаваемым ближайшими заряженными частицами (ионы кислорода О-2; хлора Cl-1 и т.д.). Это кристаллическое электрическое поле изменяет энергию электронов иона. В результате действия этого поля среднее значение орбитального момента атома  стремится к нулю, т.е.
стремится к нулю, т.е.  , поэтому для ионов 3dа
, поэтому для ионов 3dа  , и
, и  , а
, а  .
.
Для  имеем
имеем  или в магнетонах Бора
или в магнетонах Бора  (3)
(3)
Отсюда, зная величину  , можно найти a - число электронов на подоболочке иона. Кюри экспериментально установил, что магнитная восприимчивость
, можно найти a - число электронов на подоболочке иона. Кюри экспериментально установил, что магнитная восприимчивость  удовлетворяет закону
удовлетворяет закону  , где
, где  ; тогда
; тогда  ;
; 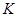 - постоянная Больцмана;
- постоянная Больцмана;  - абсолютная температура;
- абсолютная температура;  - число частиц (ионов).
- число частиц (ионов).
Если вещество, содержащее ионы с  , поместить в неоднородное магнитное поле, на вещество будет действовать сила
, поместить в неоднородное магнитное поле, на вещество будет действовать сила  , где
, где  - вектор намагничивания, равный
- вектор намагничивания, равный 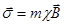 , где m – масса вещества. Если
, где m – масса вещества. Если  , то:
, то:  .
.
Полная сила  , (4)
, (4)
где S – площадь сечения ампулы, В0 – индукция магнитного поля в центре зазора,
N – число частиц в единице объема.
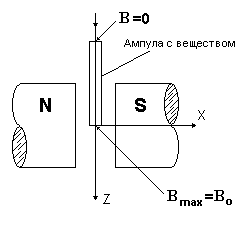 Измеряя силу FZ, зная температуру и индукцию магнитного поля можно определить зна-чение магнитного момента иона в магнетонах Бора.
Измеряя силу FZ, зная температуру и индукцию магнитного поля можно определить зна-чение магнитного момента иона в магнетонах Бора.
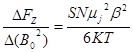 , (5)
, (5)
отсюда  . (6)
. (6)
С другой стороны из (3) следует
 .
.
 (7)
(7)
Находим  из уравнения (7), найденное значение округляем до целого числа и берем
из уравнения (7), найденное значение округляем до целого числа и берем  .
.

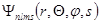 , аналитическое выражение которой зависит от квантовых чисел
, аналитическое выражение которой зависит от квантовых чисел  . Для нерелятивистского случая волновая функция
. Для нерелятивистского случая волновая функция  находится из решения уравнения Шредингера:
находится из решения уравнения Шредингера: 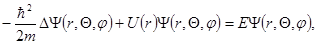
 , где
, где  - заряд ядра, Z – порядковый номер элемента (для водорода Z= 1).
- заряд ядра, Z – порядковый номер элемента (для водорода Z= 1).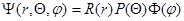 .
. , методом разделения переменных, получим выражение для R(r), P(Θ), Φ(φ) и значение
, методом разделения переменных, получим выражение для R(r), P(Θ), Φ(φ) и значение 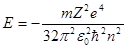 ;
; (полином Лаггера), где n =1, 2, 3,…∞;
(полином Лаггера), где n =1, 2, 3,…∞; - безразмерный параметр;
- безразмерный параметр; 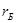 - радиус Бора (наименьшее расстояние электрона от ядра в атоме водорода).
- радиус Бора (наименьшее расстояние электрона от ядра в атоме водорода). (полином Лежандра).
(полином Лежандра). - определяют из условия нормировки
- определяют из условия нормировки  .
. , равна произведению полинома Лаггера, полинома Лежандра и
, равна произведению полинома Лаггера, полинома Лежандра и  .
. ;
; .
. ; и соответственно
; и соответственно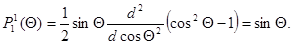
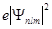 (или электронное облако, орбиталь, облако вероятности) будет иметь вид:
(или электронное облако, орбиталь, облако вероятности) будет иметь вид:
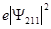
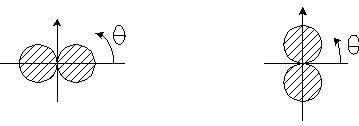
 - определяет энергию электрона в атоме; квантовое число
- определяет энергию электрона в атоме; квантовое число  - определяет величину орбитального углового момента электрона
- определяет величину орбитального углового момента электрона 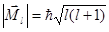 и форму электронного облака; а
и форму электронного облака; а 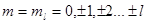 - проекцию этого углового момента на избранную ось (Z)
- проекцию этого углового момента на избранную ось (Z)  ; квантовое число
; квантовое число  - определяет собственный угловой момент электрона (спин)
- определяет собственный угловой момент электрона (спин)  ; а
; а 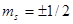 - проекцию спина на избранную ось (Z)
- проекцию спина на избранную ось (Z)  . Количество проекций орбитального углового момента электрона равно 2 l +1; спинового - 2 s +1.
. Количество проекций орбитального углового момента электрона равно 2 l +1; спинового - 2 s +1. , образуя полный орбитальный момент атома
, образуя полный орбитальный момент атома  , величина которого определяется квантовым числом L:
, величина которого определяется квантовым числом L: 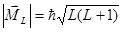 ,
,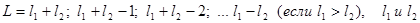 - квантовые числа орбитального углового момента первого и второго электронов. Проекция полного углового орбитального момента атома на ось Z определяется квантовым числом
- квантовые числа орбитального углового момента первого и второго электронов. Проекция полного углового орбитального момента атома на ось Z определяется квантовым числом  :
:  , где
, где  , число проекций полного углового орбитального момента атома равно
, число проекций полного углового орбитального момента атома равно  .
. , т.к.
, т.к.  , а
, а  , то квантовое число полного собственного углового момента S будет равно сумме всех
, то квантовое число полного собственного углового момента S будет равно сумме всех  с учетом их знаков. Величина собственного полного углового момента атома равна
с учетом их знаков. Величина собственного полного углового момента атома равна  .
. , равный векторной сумме
, равный векторной сумме  , где
, где  , если
, если 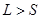 .
. . Полные угловые моменты электронов
. Полные угловые моменты электронов  , складываясь векторно, дают полный угловой момент атома
, складываясь векторно, дают полный угловой момент атома  ,
,  , если
, если  .
. где
где  (1)
(1) - гиромагнитное отношение:
- гиромагнитное отношение:  ;
;  - фактор Ланде, значения которого для свободного атома равно:
- фактор Ланде, значения которого для свободного атома равно: 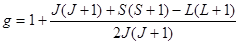 ; (2) m0 – масса покоя электрона.
; (2) m0 – масса покоя электрона. и
и 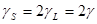 .
. , имеющего минимальную энергию.
, имеющего минимальную энергию. (с учетом того, что
(с учетом того, что  может принимать значения ±1/2). Задавая определенное значение квантового числа
может принимать значения ±1/2). Задавая определенное значение квантового числа  , мы тем самым задаем значения квантовых чисел
, мы тем самым задаем значения квантовых чисел  и
и  . Все электроны, имеющие одинаковое квантовое число
. Все электроны, имеющие одинаковое квантовое число  образуют подоболочку. Подоболочки обозначаются так:
образуют подоболочку. Подоболочки обозначаются так:  -подоболочка (
-подоболочка (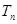 , разность двух энергетических термов определяет частоту излучаемого фотона
, разность двух энергетических термов определяет частоту излучаемого фотона 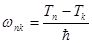 .
. могут принимать различные значения. Символ, содержащий информацию о квантовых числах
могут принимать различные значения. Символ, содержащий информацию о квантовых числах  термы обозначают буквами
термы обозначают буквами  соответственно, вверху слева от буквы, обозначающей терм, пишется число, равное
соответственно, вверху слева от буквы, обозначающей терм, пишется число, равное  , называемое мультиплетностью терма, внизу справа – квантовое число J, например
, называемое мультиплетностью терма, внизу справа – квантовое число J, например  (для этого спектрального терма:
(для этого спектрального терма:  ).
). ). Спектральный терм основного состояния находится по правилам Хунда, с учетом принципа Паули: минимальную энергию имеет атом, если его спиновое число
). Спектральный терм основного состояния находится по правилам Хунда, с учетом принципа Паули: минимальную энергию имеет атом, если его спиновое число  имеет максимальное значение, и при
имеет максимальное значение, и при  максимальным должно быть орбитальное квантовое число
максимальным должно быть орбитальное квантовое число  . Определив
. Определив  полного углового момента атома:
полного углового момента атома:  , где «+» берут, если число электронов на подоболочке больше половины, и «-», если меньше половины. Для подоболочки, заполненной наполовину
, где «+» берут, если число электронов на подоболочке больше половины, и «-», если меньше половины. Для подоболочки, заполненной наполовину  , и тогда
, и тогда  . Число электронов на подоболочке равно:
. Число электронов на подоболочке равно:  .
. , где
, где  - число нескомпенсированных электронов на подоболочке. Для подоболочки с квантовым числом
- число нескомпенсированных электронов на подоболочке. Для подоболочки с квантовым числом  , например, для ионов 3dа S=1/2(10-а).
, например, для ионов 3dа S=1/2(10-а). стремится к нулю, т.е.
стремится к нулю, т.е.  , поэтому для ионов 3dа
, поэтому для ионов 3dа  , и
, и  , а
, а  .
. имеем
имеем  или в магнетонах Бора
или в магнетонах Бора  (3)
(3) , можно найти a - число электронов на подоболочке иона. Кюри экспериментально установил, что магнитная восприимчивость
, можно найти a - число электронов на подоболочке иона. Кюри экспериментально установил, что магнитная восприимчивость  удовлетворяет закону
удовлетворяет закону  , где
, где  ; тогда
; тогда  ;
; 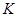 - постоянная Больцмана;
- постоянная Больцмана;  - абсолютная температура;
- абсолютная температура;  - число частиц (ионов).
- число частиц (ионов). , поместить в неоднородное магнитное поле, на вещество будет действовать сила
, поместить в неоднородное магнитное поле, на вещество будет действовать сила  , где
, где  - вектор намагничивания, равный
- вектор намагничивания, равный 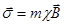 , где m – масса вещества. Если
, где m – масса вещества. Если  , то:
, то:  .
. , (4)
, (4) Измеряя силу FZ, зная температуру и индукцию магнитного поля можно определить зна-чение магнитного момента иона в магнетонах Бора.
Измеряя силу FZ, зная температуру и индукцию магнитного поля можно определить зна-чение магнитного момента иона в магнетонах Бора.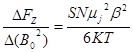 , (5)
, (5) . (6)
. (6) .
. (7)
(7) .
.


