 Если бы электроны вели себя как свободные классические частицы, то их энергия была бы равна
Если бы электроны вели себя как свободные классические частицы, то их энергия была бы равна 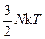 , а их вклад в теплоемкость составлял бы
, а их вклад в теплоемкость составлял бы  , где N – полное число электронов. Однако эксперименты показывали, что электронный вклад в теплоемкость при комнатной температуре составляет обычно не более 0,01 от этой величины. Противоречие было устранено лишь после открытия принципа Паули и функции распределения Ферми. В рамках квантовой теории тепловое возбуждение испытывают лишь электроны, находящиеся в состояниях с энергиями в интервале k T вблизи уровня Ферми EF = k TF (где TF – температура Ферми). Тогда тепловое возбуждение при повышении температуры от 0 до T может испытывать лишь часть их порядка ~ Т/ТF, так как приблизительно именно такая их доля обладает энергиями в интервале k T в верхней части энергетического распределения. Каждый из
, где N – полное число электронов. Однако эксперименты показывали, что электронный вклад в теплоемкость при комнатной температуре составляет обычно не более 0,01 от этой величины. Противоречие было устранено лишь после открытия принципа Паули и функции распределения Ферми. В рамках квантовой теории тепловое возбуждение испытывают лишь электроны, находящиеся в состояниях с энергиями в интервале k T вблизи уровня Ферми EF = k TF (где TF – температура Ферми). Тогда тепловое возбуждение при повышении температуры от 0 до T может испытывать лишь часть их порядка ~ Т/ТF, так как приблизительно именно такая их доля обладает энергиями в интервале k T в верхней части энергетического распределения. Каждый из 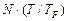 электронов обладает приобретенной тепловой энергией порядка k T, а полная энергия Δ E теплового возбуждения электронов составляет величину порядка
электронов обладает приобретенной тепловой энергией порядка k T, а полная энергия Δ E теплового возбуждения электронов составляет величину порядка  . Электронную теплоемкость
. Электронную теплоемкость  получаем, дифференцируя энергию по температуре:
получаем, дифференцируя энергию по температуре:
 . (24)
. (24)
Отсюда следует, что электронная теплоемкость линейно зависит от температуры в полном соответствии с экспериментом. С учетом того, что температура Ферми TF ~ 5 . 104 К, оценим величину электронной теплоемкости для одновалентных металлов. Величина  при комнатной температуре получается примерно в сто раз меньше классического значения (3/2) . R.
при комнатной температуре получается примерно в сто раз меньше классического значения (3/2) . R.
Более строгий расчет приводит к следующему выражению для электронной теплоемкости:
 . (25)
. (25)
Коэффициент γ называется коэффициентом электронной теплоемкости.
При достаточно низких температурах электронная доля теплоемкости становится больше доли решетки, так как последняя изменяется по закону T 3 (рис. 4). В результате ниже некоторой температуры электронный вклад в теплоемкость металлов будет всегда преобладать.

 Если бы электроны вели себя как свободные классические частицы, то их энергия была бы равна
Если бы электроны вели себя как свободные классические частицы, то их энергия была бы равна 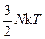 , а их вклад в теплоемкость составлял бы
, а их вклад в теплоемкость составлял бы  , где N – полное число электронов. Однако эксперименты показывали, что электронный вклад в теплоемкость при комнатной температуре составляет обычно не более 0,01 от этой величины. Противоречие было устранено лишь после открытия принципа Паули и функции распределения Ферми. В рамках квантовой теории тепловое возбуждение испытывают лишь электроны, находящиеся в состояниях с энергиями в интервале k T вблизи уровня Ферми EF = k TF (где TF – температура Ферми). Тогда тепловое возбуждение при повышении температуры от 0 до T может испытывать лишь часть их порядка ~ Т/ТF, так как приблизительно именно такая их доля обладает энергиями в интервале k T в верхней части энергетического распределения. Каждый из
, где N – полное число электронов. Однако эксперименты показывали, что электронный вклад в теплоемкость при комнатной температуре составляет обычно не более 0,01 от этой величины. Противоречие было устранено лишь после открытия принципа Паули и функции распределения Ферми. В рамках квантовой теории тепловое возбуждение испытывают лишь электроны, находящиеся в состояниях с энергиями в интервале k T вблизи уровня Ферми EF = k TF (где TF – температура Ферми). Тогда тепловое возбуждение при повышении температуры от 0 до T может испытывать лишь часть их порядка ~ Т/ТF, так как приблизительно именно такая их доля обладает энергиями в интервале k T в верхней части энергетического распределения. Каждый из 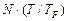 электронов обладает приобретенной тепловой энергией порядка k T, а полная энергия Δ E теплового возбуждения электронов составляет величину порядка
электронов обладает приобретенной тепловой энергией порядка k T, а полная энергия Δ E теплового возбуждения электронов составляет величину порядка  . Электронную теплоемкость
. Электронную теплоемкость  получаем, дифференцируя энергию по температуре:
получаем, дифференцируя энергию по температуре: . (24)
. (24) . (25)
. (25)


