Теоретическая часть. 16. Най­ди­те пло­щадь пря­мо­уголь­ни­ка ABCD, счи­тая сто­ро­ны квад­рат­ных кле­ток рав­ны­ми 1.

16. Най­ди­те пло­щадь пря­мо­уголь­ни­ка ABCD, счи­тая сто­ро­ны квад­рат­ных кле­ток рав­ны­ми 1.

17. Най­ди­те пло­щадь пря­мо­уголь­ни­ка , если его пе­ри­метр равен 18, и одна сто­ро­на на 3 боль­ше дру­гой.

18. Най­ди­те диа­го­наль квад­ра­та , если его пло­щадь равна 2.

19. Как изменится площадь и периметр квадрата, если его диагональ увеличить в 4 раза?

20. Се­ре­ди­ны сто­рон пря­мо­уголь­ни­ка 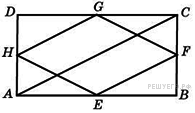, диа­го­наль ко­то­ро­го равна 5, по­сле­до­ва­тель­но со­еди­не­ны от­рез­ка­ми. Най­ди­те пе­ри­метр об­ра­зо­вав­ше­го­ся че­ты­рех­уголь­ни­ка.

 

Теоретическая часть.

Четырёхугольники

Трапеции

Параллелограммы Параллелограмм

Прямоугольники

Ромбы

Квадраты

 

Параллелограммом называется четырёхугольник, у которого каждые две противолежащие стороны параллельны.

Свойства параллелограмма.		Признаки параллелограмма
1. Противолежащие стороны параллелограмма равны. 2.Противолежащие углы параллелограмма равны. 3.Диагонали параллелограмма точкой пересечения делятся пополам.	1.Если в четырёхугольнике две противолежащие стороны равны и параллельны, то этот четырёхугольник параллелограмм. 2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм. 3.Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

Прямоугольником называется параллелограмм, у которого все углы прямые.

Свойства прямоугольника.		Признаки прямоугольника.
1.Диагонали прямоугольника равны.	1.Если один из углов параллелограмма прямой, то этот параллелограмм – прямоугольник. 2.Если диагонали параллелограмма равны, то этот параллелограмм – прямоугольник.

Ромбом называется параллелограмм, у которого все стороны равны.

Свойства ромба.		Признаки ромба.
1.Диагонали ромба перпендикулярны, и являются биссектрисами его углов	1.Если диагонали параллелограмма перпендикулярны, то этот параллелограмм – ромб.

Квадратом называется прямоугольник, у которого все стороны равны; либо квадратом называется ромб, у которого все углы прямые.

Замечание: исходя из определения, квадрат имеет все свойства прямоугольника и ромба.

 

Теорема 2. Противолежащие стороны параллелограмма равны.

В С Дано:АВСD - параллелограмм.

А D Доказать:АВ = СD и ВС = АD.

Доказательство:1) Проведем диагональ АС;2) Δ АВС и Δ АСD равны по второму признаку равенства треугольников; 3) Т.о. АВ = СD.