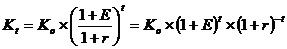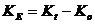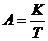Инвестиции и время
4.1 Понятие о дисконтировании. Модель начисления сложных процентов. Дисконтирование по сложным ставкам
Одна из главных проблем при расчете инвестиций состоит в том, чтобы сопоставить выплаты, которые делаются в разные моменты времени. Одинаковые по величине затраты, осуществляемые в разное время, экономически неравнозначны. С указанной проблемой связано определение наращенной или будущей стоимости инвестиций. Процент роста основной суммы вклада за счет накопления процентов называется начислением сложного процента, а сумма, полученная в результате накопления процентов, называется наращенной или будущей стоимостью суммы вклада по истечении периода, за который осуществляется расчет. Первоначальная сумма вклада называется текущей стоимостью. Процесс расчета будущей стоимости средств, инвестируемых сегодня, является одной из разновидностей особого типа финансовых расчетов и относится к дисконтированию. Модель сложных процентов в общем виде может быть записана:
где
E – величина доходности наших инвестиций, которая равна ставке банковского процента (норма дисконта); t – число стандартных периодов времени, в течение которых наши инвестиции будут участвовать в коммерческом обороте. В финансовой практике часто сталкиваются с задачей обратной определению наращенной суммы: по заданной сумме Дисконтирование – это приведение разновременных экономических показателей к какому-либо одному моменту времени. Разновидностью дисконтирования является обратный расчет ценности денег, то есть определение того, сколько надо было бы инвестировать сегодня, чтобы получить некоторую сумму в будущем. Это называется расчетом текущей (современной) стоимости, или определением приведенной дисконтируемой стоимости:
где Эта формула приобретает смысл, если норма дисконта будет здесь обозначать тот уровень дохода, который мы реально можем себе обеспечить, вложив средства в доступный для нас проект инвестирования. В теоретической основе модели расчета текущей стоимости лежит концепция арбитражного ценообразования. Смысл этой концепции состоит в том, что можно получать выгоду за счет использования несовершенств рынка (возможное существование разных цен на один и тот же товар, но на разных территориально удаленных рынках позволяет одновременно заключить сделку о покупке товара по низкой цене на одном рынке и продавать его по более высокой цене на другом рынке). Но такие операции обеспечивают выгоду только в краткосрочном плане. В более длительной перспективе деятельность арбитражеров приводит к устранению несовершенств рынка и выравниванию цен. Действия на основе арбитражной теории ценообразования может привести к постепенному выравниванию цен, которые инвесторы соглашаются уплатить сегодня за получение идентичных денежных притоков в равно удаленном будущем. При оценке эффективности инвестиционного проекта, соизмерение разновременных показателей осуществляется путем приведения (дисконтирования) их к ценности в начале периода (t = 0). Для приведения разновременных затрат, результатов и эффектов используется норма дисконта (Е), равная норме дохода на капитал, приемлемой для инвестора. Техническое приведение к базисному моменту времени затрат, результатов и эффектов удобно производить путем их умножения на коэффициент дисконтирования
где t – номер счета расчета (t = 0, 1, 2, 3….). Если же норма дисконта меняется во времени и на шаге расчета t = E, то коэффициент дисконтирования равен:
Сумма дисконтирования имеет вид:
где К – постоянный платеж.
Результат сравнения двух проектов с различным распределением эффекта во времени может существенно зависеть от нормы дисконта. В рыночной экономике эта величина определяется исходя из депозитного процента по вкладам (в постоянных ценах). На практике она принимается большей его значения за счет инфляции и риска, связанного с инвестициями. Если принять норму дисконта ниже депозитного процента, то инвесторы предпочтут вкладывать деньги в банк, а не в производство. Если же норма дисконта станет выше депозитного процента на величину большую, чем та, которая оправдывается инфляцией и инвестиционным риском, то возникает перетекание денег в инвестиции, повышенный спрос на них и как следствие – повышение их цены, то есть банковского процента. Эта оценка нормы дисконта справедлива для собственного капитала. В случае когда весь капитал является заемным, норма дисконта представляет собой соответствующую процентную ставку, определенную условиями процентных выплат и погашению займов. Когда капитал смешанный, норма дисконта приближенно может быть найдена как средневзвешенная стоимость капитала, рассчитанная с учетом структуры капитала:
где n – виды капитала,
В период высокой инфляции депозитный процент по вкладам не определяет реальную цену денег. В связи с этим можно использовать два подхода. 1. Для оценки народно-хозяйственной, т.е. экономической эффективности. Здесь норма дисконта должна отражать не только чисто финансовые интересы государства, но и систему предпочтений членов общества по поводу относительной значимости доходов в различные моменты времени, в том числе и с учетом социальных и экономических результатов. Данная оценка является «социальной нормой дисконта» и должна устанавливаться государством как специфический социально-экономический норматив, обязательный для оценки проектов, в которых государству предполагается принять участие. 2. Для оценки коммерческой эффективности. Здесь каждый хозяйствующий субъект сам оценивает свою индивидуальную «цену денег», т.е. выраженную в долях единицы реальную норму годового дохода на вложенный капитал с учетом альтернативных и доступных на рынке направлений вложений со сравнимым риском. Корректируя ее с учетом риска, связанного с конкретным проектом, субъект может определить и индивидуальную норму дисконта. Однако в современных условиях при неразвитом фондовом рынке, такой подход затруднителен, хотя и возможен. Он может привести к ошибочным решениям, если субъект в качестве альтернативы будет принимать вложения средств в краткосрочные спекулятивные операции (с иностранной валютой, импортные и дефицитные товары), то в этих условиях определенным ориентиром при установлении индивидуальной нормы дисконта может служить депозитный процент по вкладам в относительно стабильной иностранной валюте, хотя и здесь надо учитывать инфляцию и риск банкротства коммерческих банков, которые принимают соответствующие депозиты.
4.2 Аннуитет и перпетуитет. Модель Гордона
Аннуитет – это последовательность из t денежных потоков по одному в каждом периоде. Под аннуитетом также понимается ежегодный взнос денежных средств ради накопления определенной суммы в будущем Дополнительно Дополнительно Дополнительно Классическим примером такого рода операций является накопление амортизационного фонда, т.е. денежного фонда, позволяющего приобрести новое оборудование взамен постепенно изнашивающегося старого. Формула для нахождения текущей стоимости аннуитета имеет вид:
где А – обыкновенный равномерный платеж. Такой аннуитет называется стандартным. Если первый платеж происходит в конце периода 1, мы имеем обыкновенный аннуитет. Когда же платежи происходят в начале каждого периода, то это авансовый аннуитет. Если осуществляется серия равных платежей, то аннуитет определяется по формуле:
При оценке инвестиционных проектов, когда решается вопрос о предельно допустимой сумме вложений, то на эту проблему полезно посмотреть с точки зрения альтернативного дохода, обеспечиваемого вложениями рентного типа. Примером такого рода альтернативного вложения средств является банковский бессрочный текущий счет, процентный доход по которому полностью изымается сразу после его начисления. Такой вид инвестиций для противопоставления аннуитету называется перпетуитетом. Перпетуитет - это аннуитет, который никогда не кончается и определяется по формуле:
Перпетуитеты редко встречаются в реальной жизни, но они позволяют определить стоимость в предельных случаях. Особый случай перпетуитета – инвестиция с неограниченным сроком жизни, но с постоянно возрастающими величинами годового дохода. Если такой рост происходит с темпом равным q, а РМТ1 будет обозначать ожидаемую величину денежных поступлений в конце первого года, тогда текущая (современная) стоимость такой инвестиции может быть определена с помощью модели Гордона:
Моделью Гордона при расчетах необходимо пользоваться аккуратно. Во-первых, надо обратить внимание на то, что в числителе стоит выражение с индексом периода 1, а не 0, так как отправной точкой расчетов является платеж по инвестируемым средствам на конец первого периода их использования. Если же платеж поступает инвестору немедленно, то его сумму следует прибавить к величине текущей стоимости, найденной по основной формуле. Во-вторых, модель Гордона можно использовать только в том случае, если поток денежных поступлений возрастает постоянно и с одним и тем же темпом роста q. В-третьих, модель гордона справедлива лишь тогда, когда темп роста q меньше, чем коэффициент дисконтирования Е. Коэффициент аннуитета (Кан) распределяет сумму Ко, для которой сейчас наступил, срок погашения, в равные суммы платежей (аннуитеты) К с учетом процента на t лет, т.е. превращает «разовый платеж сейчас» в платежный ряд. Тогда аннуитет будет равен:
Откуда коэффициент аннуитета равен:
На практике очень часто встречается ситуация, когда необходимо распределить остаточную стоимость инвестиционного платежа. Коэффициент распределения остаточной стоимости распределяет разовый платеж, который должен быть выплачен через t лет с учетом процента на этот период, тем самым превращает разовый платеж через t лет в платежный ряд. Выяснить какому ряду это соответствует можно по формуле:
где
Коэффициент конечной стоимости (коэффициент сумм начисления сложных процентов) начисляет сложные проценты на элементы платежного ряда с учетом процентов и одновременно прибавляет конечную стоимость, т.е. превращает платежный ряд в разовый платеж через t лет:
4.3 Учет инфляции при инвестировании
Инфляция – это повышение общего (среднего) уровня цен в экономике или на данный вид ресурсов (продукции, услуг). Основное влияние на показатели коммерческой эффективности инвестиционного проекта оказывает неординарность инфляции, т.е. различная величина ее уровня по видам продукции и ресурсов, а также превышение инфляции над ростом курса иностранной валюты. Помимо этого, даже однородная инфляция влияет на показатели инвестиционного проекта за счет: – изменения влияния запасов и задолженностей (увеличение запасов материалов и кредиторской задолженности становится более выгодным, а запасов готовой продукции и дебиторской задолженности – менее выгодным, чем без инфляции); – завышение налогов за счет отставания амортизационных отчислений от тех, которые соответствовали бы повышающимся ценам на основные фонды; – изменение фактических условий предоставления займов и кредитов. Наличие инфляции влияет на показатели проекта не только в денежном, но и в натуральном выражении. Инфляция приводит не только к переоценке финансовых результатов осуществленного проекта, но и к изменению самого плана реализации проекта. Поэтому переход в расчетах к твердой валюте или вообще к натуральным показателям не отменяет необходимости учета влияния инфляции. Наряду с расчетами в постоянных или мировых ценах необходимо производить расчет в прогнозных ценах с тем, чтобы максимально учесть это влияние. При уточненной оценке эффективности инвестиционного проекта необходимо учитывать динамику: – уровня роста или падения отношения курсов внутренней и иностранной валют; – общую инфляцию; – инфляцию на сбыт, т.е. цен на производимую продукцию на внутренних и внешних рынках; – цен ни используемые ресурсы и комплектующие; – прямых издержек по видам; – инфляцию на заработную плату (уровень заработной платы по видам работников); – инфляцию на общие и административные издержки; – стоимости основных фондов (земли, здания, сооружения, оборудования); – затрат на организацию сбыта (реклама, транспорт); – изменение банковского процента. При наличии информации о ценовой политике государства (на период осуществления инвестиционного проекта) расчеты эффективности могут быть выполнены в прогнозных ценах, с использованием дифференцированных по группам ресурсов, индексов изменения цен. Для того чтобы правильно оценить результаты проекта, а также обеспечить сравнимость показателей проектов в различных условиях, необходимо максимально учесть влияние инфляции на расчетные значения результатов и затрат. Для этого следует потоки затрат и результатов производить в прогнозных (текущих) ценах, а при вычислении интегральных показателей переходить к расчетным ценам, т.е. ценам, очищенным от общей инфляции. Расчетные цены приводятся к некоторому моменту времени, т.е. соответствуют ценам в этот момент, хотя могут не совпадать с ними за счет неоднородности инфляции. Расчетные цены приводятся к моменту t = 0, это необходимо при сравнении проектов с различными сроками их начала. Приведение цен ресурса «j» в момент t = t
где
В зарубежной инвестиционной практике поправка на инфляцию цены определяется по формуле:
где Ц(б) – базовая цена товара;
В – доля прочих не вошедших в число
Для повышения точности формулы необходимо, чтобы возможно большее количество ресурсов (особенно с высокими ожидаемыми индексами роста цен) попало в число
Сумму начисленных процентов можно выразить формулой:
а инфляционную сумму:
Из этих формул следует, что при Е = r сумма начисленных процентов покрывает лишь потери от инфляции, а величина подлинного вознаграждения инвестору за вложенный капитал равна нулю. И только когда процентная ставка на капитал превышает уровень инфляции, инвестор действительно получает определенное вознаграждение. Распространенным методом компенсации потерь от инфляции является индексация ставки процента, по которой производится наращение. Она сводится к увеличению ставки процентов на величину, так называемой инфляционной премии. Ставку с поправкой на инфляцию называют брутто – ставкой, она определяется:
Брутто-ставка – это по существу реальная процентная ставка, которая учитывает инфляцию.
4.4 Амортизация и инвестирование
Полезный срок службы большинства видов оборудования больше года. Фактически расходы на покупку инвестиционных товаров и их производительный срок службы не попадает в один и тот же период учета. Поэтому в целях недопущения занижения прибыли, а, следовательно, и всего дохода в период покупки, с одной стороны, и завышение прибыли и дохода в последующие годы, с другой, предприятия рассчитывают полезный срок службы оборудования и распределяют общий объем стоимости инвестиционных товаров более или менее равномерно на весь срок службы оборудования. Ежегодные отчисления, которые показывают объем капитала, потребленного в ходе производства в отдельные годы, называется амортизацией. Амортизация представляет собой бухгалтерскую запись, предназначенную для того, чтобы дать более точный отчет о доходе в виде прибыли, и, следовательно, о валовом доходе компании в каждом году. Ежегодные амортизационные отчисления на реновацию оборудования определяются умножением стоимости оборудования на норму амортизации или на коэффициент амортизационных отчислений. Если равномерно распределить амортизационные отчисления за весь срок службы объекта, то коэффициент амортизации определяется по формуле:
где Т – срок службы объекта. Существует другая формула для определения коэффициента амортизации, ее предложил Лурье, и она имеет вид:
Сущность этой формулы заключается в том, что сумма амортизационных отчислений должна быть равна восстановительной стоимости объекта. Вычисленная обычным способом величина амортизационных отчислений равна:
где К - стоимость объекта; Т – срок службы объекта. Однако ежегодно осуществляемые амортизационные отчисления неравносильны через Т лет стоимости объекта. Сумма амортизационных отчислений за весь за срок службы будет больше величины стоимости объекта, так как вложенная в банк она будет приносить ежегодный процент на капитал. Для правильного сравнения вариантов затраты на возмещение износившихся основных фондов должны приравниваться к таким ежегодным расходам, которые за весь срок службы объекта вместе с процентами составят сумму, равную стоимости основных фондов. Формула Лурье не учитывает инфляцию, чтобы ее учесть необходимо в формуле номинальную процентную ставку Е заменить на реальную процентную ставку Ер, учитывающую инфляцию. Коэффициент амортизационных отчислений с учетом инфляции примет вид:
4.5 Основные требования к исходным данным, связанным с оценкой экономической эффективности инвестиционных проектов
Расчет экономических и финансовых характеристик инвестиционного проекта требует знание достаточно большого количества исходных данных об инвестиционном проекте. В соответствии с принятой практикой инвестиционный проект обычно исследуется в динамике за период, охватывающий все фазы своего осуществления. Следовательно, исходные данные должны отражать временную динамику реализации проекта. Необходимо иметь представления об экономической конъюнктуре, непосредственно связанной с производством и сбытом продукции: рынки сбыта, возможная конкуренция, тенденции изменения цен на производственную продукцию, основное сырьё и материалы, тенденции изменения других затрат. Нужно учитывать вероятные сценарии общеэкономического развития, которые выражаются в инфляции, тенденциях изменения ставки банковского процента по различным видам кредита, курса рубля по отношению к иностранной валюте.
|


 – будущая величина той суммы, которая инвестируется в любой форме сегодня и которой будем располагать через интересующий нас период времени;
– будущая величина той суммы, которая инвестируется в любой форме сегодня и которой будем располагать через интересующий нас период времени; – текущая величина той суммы, которую мы инвестируем для получения дохода в будущем;
– текущая величина той суммы, которую мы инвестируем для получения дохода в будущем; – коэффициент начисления сложных процентов Дополнительно Дополнительно Дополнительно
– коэффициент начисления сложных процентов Дополнительно Дополнительно Дополнительно
 – дисконтированный множитель за t лет или коэффициент текущей стоимости.
– дисконтированный множитель за t лет или коэффициент текущей стоимости.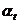 , определяемый для постоянной нормы дисконта:
, определяемый для постоянной нормы дисконта:
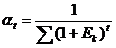

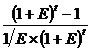 – коэффициент суммы дисконтирования.
– коэффициент суммы дисконтирования.
 – стоимость каждого из видов капитала,
– стоимость каждого из видов капитала, – доля в общем капитале каждого из видов капитала.
– доля в общем капитале каждого из видов капитала.



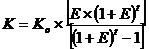


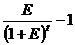 – коэффициент распределения остаточной стоимости.
– коэффициент распределения остаточной стоимости.
 к ценам того же ресурса в конце t – ого шага по прогнозным ценам проводится по формуле:
к ценам того же ресурса в конце t – ого шага по прогнозным ценам проводится по формуле:
 – цена ресурса j на t – ом шаге (прогнозная или текущая);
– цена ресурса j на t – ом шаге (прогнозная или текущая); – цена того же ресурса в ценах момента t0 (базисная цена).
– цена того же ресурса в ценах момента t0 (базисная цена).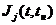 – индекс цен на ресурс «j».
– индекс цен на ресурс «j».
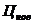 – прогнозная цена предложения товара;
– прогнозная цена предложения товара; – индексы роста цен ресурса
– индексы роста цен ресурса  . В итоге наращенная сумма к концу этого срока с учетом ее обеспечения в связи с инфляцией составит:
. В итоге наращенная сумма к концу этого срока с учетом ее обеспечения в связи с инфляцией составит: