Финансовые механизмы начисления процентов.
Существуют два механизма начисления процентов: 1. Механизм простых процентов (когда проценты начисляются только на первоначальную сумму капитала). 2. Механизм сложных процентов (когда проценты начисляются не только на первоначальную сумму, но и на проценты, начисленные в предыдущий период). Условные обозначения: 1. Первоначальная стоимость капитала (PV). 2. Будущая стоимость капитала (FV). 3. Время (период), выраженное в годах (n). 4. Годовая процентная ставка (i). 5. Частота начисления процентов в течение календарного года (k). 6. Частота платежей в течение календарного года (m). 7. Величина платежа аннуитета (PMT). С помощью простых процентов можно определить только будущую стоимость капитала, при этом простые проценты не предполагают ни пополнения счета в банке, ни увеличения частоты начисления процентов банком. Формула для расчета простых процентов: FV = PV (1 + i × n) Сложные проценты имеют шесть функций: 1. Будущая стоимость капитала: ü если k = 1: ü если k > 1:
Оценка инвестиций. Лекция (22.04.14) Продолжение предыдущей лекции (финансовые механизмы начисления процентов): Пример 1: Вкладчик положил в банк 30 тыс. у.е. под 10% годовых. Определить аккумулированную сумму через 4 года, если проценты банк будет начислять ежеквартально и ежемесячно.
2. Будущая стоимость аннуитета. Используется в тех случаях, когда речь идет не о разовом платеже, а о серии регулярных платежей (аннуитетных платежей) и необходимо узнать в будущем накопленную сумму: ü если k = 1 и m = 1: ü если k = 1 и m > 1: ü если k > 1 и m = 1: ü если k > 1 и m > 1: Пример 2: Предпринимателю предстоит через 2 года и 3 квартала купить недвижимость, которая будет стоить 410 тыс. у.е. Сегодня он имеет возможность депонировать на свой счет в банке ежемесячно по 10 тыс. у.е. под 14% годовых. Рассчитать достаточность накоплений.
Нужно искать более высокую процентную ставку или депонировать большую сумму. Пример 3: Помещение сдается в аренду на 5 лет. Арендные платежи вносятся ежегодно на счет владельца помещения в размере 300 тыс. у.е. Банк на внесенные суммы начисляет 13% годовых. Какова станет накопленная сумма к концу срока аренды?
3. Фонд возмещения капитала. Используется в тех случаях, когда известна желаемая будущая сумма, которую надо накопить, и необходимо узнать размер аннуитетных платежей: ü если k = 1 и m = 1: ü если k = 1 и m > 1: ü если k > 1 и m = 1: ü если k > 1 и m > 1: Пример 4: Владелец дома планирует провести капитальный ремонт через 6 лет и предполагает, что это будет стоить 70 тыс. у.е. Чтобы накопить эту сумму ему необходимо в конце каждого года депонировать некий платеж в банк под 10% годовых. Какова величина этой суммы?
Пример 5: Через 4 года у предприятия появится возможность выкупить завод по производству деревообрабатывающих изделий стоимостью 2300 тыс. у.е. Чтобы накопить эту сумму предприниматель готов ежеквартально депонировать на свой счет в банке некую сумму под 12% годовых с начислениями по полугодиям. Какова должна быть величина этой суммы?
Оценка инвестиций. Лекция (29.04.14) Продолжение предыдущей лекции (финансовые механизмы начисления процентов): 4. Текущая стоимость капитала. Используется в тех случаях, когда будущую стоимость капитала нужно пересчитать к настоящему моменту времени: ü если k = 1: ü если k > 1: Пример 6: Предприниматель приобрел опцион на покупку земельного участка, который дает ему право купить 150 га земли по цене 7000 у.е. за 1 га через 3 года. Какую сумму предприниматель должен сегодня положить в банк под 10% годовых с ежеквартальным начислением процентов, чтобы к концу 3-го года на счет в банке была требуемая сумма?
5. Текущая стоимость аннуитета. Используется в тех случаях, когда есть серия аннуитетных будущих платежей (доходов) и их необходимо пересчитать или перевести к настоящему моменту времени: ü если m = 1: ü если m > 1: 6. Ипотечная постоянная. Позволяет узнать размер аннуитетного платежа по взятому кредиту (PV – кредит): ü если m = 1: ü если m > 1: Пример 7: Приобретается квартира по договору ипотечного кредитования стоимостью 8000000 руб. Величина кредита составляет 75% от стоимости квартиры. Срок кредита возможен на 10 и 20 лет, процентная ставка – 14% годовых. Кредит предполагается погашать ежемесячно. Определить размер платежи.
Переплата: 1. 84000 × 12 × 10 = 10080000 руб. 2. 66000 × 12 × 20 = 15840000 руб.
|

 ;
; .
.
 = 48141,19 у.е.
= 48141,19 у.е. = 48366,78 у.е.
= 48366,78 у.е. ;
; ;
; ;
; .
. = 401975,84 у.е.
= 401975,84 у.е. = 1944081,183 у.е.
= 1944081,183 у.е. ;
; ;
; ;
; .
. = 9067,36 у.е.
= 9067,36 у.е. = 113261,7 у.е. в квартал.
= 113261,7 у.е. в квартал. ;
; .
. = 787500 у.е.
= 787500 у.е. ;
; .
. ;
;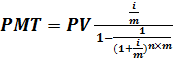 .
. = 84000 руб. / мес.
= 84000 руб. / мес. = 66000 руб. / мес.
= 66000 руб. / мес.


