Теорема 3. (Интегральный признак сходимости ряда)
Пусть члены ряда Тогда справедливы следующие утверждения: 1) если несобственный интеграл 2) если указанный интеграл расходится, то расходится и ряд (1). Пример 8. Исследовать сходимость ряда Решение. Пусть
то есть несобственный интеграл 1-го рода сходится, тогда данный ряд сходится.
Знакопеременные ряды. Абсолютная и условная сходимости. Аудиторное задание 1. Доказать сходимость следующих рядов и найти их суммы: а) (Ответ: а) 2. Исследовать на сходимость следующие ряды; а) в) д)
3. Доказать: а)
4. Исследовать сходимость следующих рядов с помощью интегрального признака Коши:
а)
Домашнее задание 1. 2. 3.
4. 5. (Ответ: 6. Литература. 1. А.П. Рябушко, В.В. Бархатов, В.В. Державец, И.Е. Юруть, Индивидуальные задания по высшей математике, - Мн.: Выш. Шк., 2000, 303 с. 2. А.П. Рябушко, В.В. Бархатов, В.В. Державец, И.Е. Юруть, Индивидуальные задания по высшей математике, Часть 2- Мн.: Выш. Шк., 2002, 396 с. 3. А.П. Рябушко, В.В. Бархатов, В.В. Державец, И.Е. Юруть, Индивидуальные задания по высшей математике, Часть 3- Мн.: Выш. Шк., 2002, 288 с. 4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, Ч.1: Учеб. Пособие для втузов. – М.: Высш. Школа, 1999, - 304 с. 5. Сборник задач по математике для втузов. Линейная алгебра и основы математического анализа, под редакцией А.В. Ефимова, Б.П. Демидовича.– М.: Наука, 1981, 464 с.
|

 (1) положительны и не возрастают, т.е.
(1) положительны и не возрастают, т.е.  и пусть
и пусть  - такая непрерывная, положительная и невозрастающая функция, что
- такая непрерывная, положительная и невозрастающая функция, что 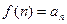 ,
, 
 сходится, то и сходится и ряд (1).
сходится, то и сходится и ряд (1).
 . Применим интегральный признак. Так как
. Применим интегральный признак. Так как ,
, ; б)
; б) 
 ; б)
; б) 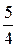 ).
). ; б)
; б)  ;
; ; г)
; г)  ;
; ; е)
; е)  .
. ; б)
; б) 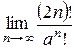 при
при 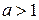 .
. ; б)
; б)  ; в)
; в) 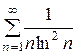 .
. доказать сходимость ряда и найти его сумму. (Ответ:
доказать сходимость ряда и найти его сумму. (Ответ:  )
) исследовать сходимость ряда.
исследовать сходимость ряда. доказать сходимость ряда и найти его сумму.
доказать сходимость ряда и найти его сумму. исследовать сходимость ряда.
исследовать сходимость ряда. доказать сходимость ряда и найти его сумму.
доказать сходимость ряда и найти его сумму. )
) исследовать сходимость ряда.
исследовать сходимость ряда.


