Сходимость положительных рядов.
Это ряды, члены которых неотрицательны.
Тогда По теореме о пределе монотонной последовательности следует: Утверждение. Положительный ряд всегда имеет сумму. Эта сумма будет конечной (и следовательно, ряд будет сходиться), если частичные суммы ряда ограничены сверху, и бесконечной (а ряд расходиться) в противном случае. (Все признаки сходимости положительных рядов основаны на этой теореме). Теоремы сравнения рядов. Сходимость или расходимость положительного ряда часто устанавливают путем сравнения его с другим рядом, заведомо сходящимся или расходящимся. Теорема 1 (первая теорема сравнения). Пусть даны два положительных ряда
Если, хотя бы начиная с некоторого номера Теорема 2 (вторая теорема сравнения). Если существует Таким образом, при Достаточные признаки сходимости положительных рядов. Теорема 1 (Признак Даламбера). Пусть дан ряд Тогда, если существует предел То 1) ряд сходится в случае 2) ряд расходится в случае
В случае Пример 6. Исследовать сходимость ряда Решение.Так как
Ряд сходится. Теорема 2. (Признак Коши). Рассмотрим ряд Если существует предел То, 1) в случае 2) в случае В случае Пример 7. Исследовать сходимость ряда Решение. Так как
Поэтому данный ряд сходится.
|

 ,
,  ,
, 
 т.е.
т.е.  – возрастающая последовательность.
– возрастающая последовательность. (В)
(В) выполняется
выполняется  , то из сходимости ряда (В) вытекает сходимость ряда (А) или из расходимости ряда (А) следует расходимость ряда (В).
, то из сходимости ряда (В) вытекает сходимость ряда (А) или из расходимости ряда (А) следует расходимость ряда (В).
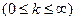 , то из сходимости ряда (В) при
, то из сходимости ряда (В) при 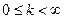 вытекает сходимость ряда (А), а из расходимости ряда (В) при
вытекает сходимость ряда (А), а из расходимости ряда (В) при  вытекает расходимость ряда (А).
вытекает расходимость ряда (А). оба ряда сходятся или расходятся одновременно.
оба ряда сходятся или расходятся одновременно. ,
, 

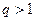
 ответа на вопрос о сходимости или расходимости ряда теорема не дает.
ответа на вопрос о сходимости или расходимости ряда теорема не дает.
 , тогда
, тогда .
.

 , то применяя признак Коши
, то применяя признак Коши .
.


