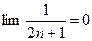Знакочередующиеся ряды. Теорема Лейбница
Практическое занятие 9-2часа Знакочередующиеся ряды. Знакопеременные ряды Знакочередующиеся ряды. Теорема Лейбница Рассмотрим ряды, члены которых имеют чередующиеся знаки, т.е.
Теорема (Лейбница). Если в знакочередующемся ряде (1) члены Определение. Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные (количество положительных и количество отрицательных членов бесконечно, т.к. если конечное плюс бесконечное, то можно отбросить конечное число членов). Знакочередующиеся ряды являются частным случаем знакопеременных рядов.
Рассмотрим знакопеременный ряд
и ряд, составленный из абсолютных величин
Определение. Ряд (1) называется абсолютно сходящимся, если сходится ряд из абсолютных величин (2).
Теорема 1 (достаточный признак сходимости знакопеременного ряда). Если ряд (1) сходится абсолютно, то он сходится. Замечание. Теорема 1 является достаточным признаком сходимости знакопеременного ряда, но не необходимым: Существуют такие знакопеременные ряды, которые сами сходятся, но ряды, составленные из абсолютных величин их членов, расходятся. Введем понятие условной сходимости знакопеременного ряда. Определение. Ряд (1) называется условно сходящимся, если ряд из абсолютных величин
Пример 9. Исследовать сходимость ряда.
то
Следовательно, выполнено первое условие признака Лейбница. Далее, так как
то выполнено и второе условие. Значит, данный ряд сходится.
Пример 10. Исследовать сходимость ряда
С другой стороны, Так как Пример 11. Исследовать сходимость ряда
По признаку Даламбера имеем
Следовательно, ряд сходится абсолютно.
Пример 12. Исследовать сходимость ряда
Так как Исследуем на условную сходимость: так как 1) 2) То по признаку Лейбница ряд сходится условно.
|


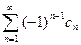 (1), где
(1), где  . Такой ряд называется знакочередующимся.
. Такой ряд называется знакочередующимся.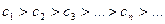 (2) - условие монотонного убывания и
(2) - условие монотонного убывания и  . То ряд (1) сходится, его сумма положительна и не превосходит первого члена.
. То ряд (1) сходится, его сумма положительна и не превосходит первого члена.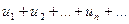 (1)
(1)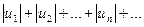 (2)
(2)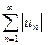 расходится, а ряд
расходится, а ряд 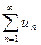 сходится.
сходится.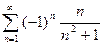 .
.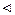 Применим признак Лейбница. Так как
Применим признак Лейбница. Так как
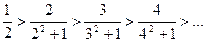
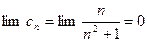

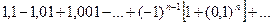
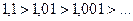
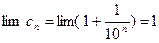
 , то не выполнен необходимый признак сходимости ряда. Ряд расходится.
, то не выполнен необходимый признак сходимости ряда. Ряд расходится. 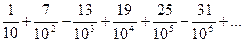
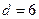 , то
, то 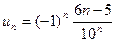 . Исследуем на абсолютную сходимость:
. Исследуем на абсолютную сходимость: 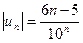
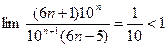
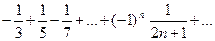

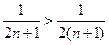 и ряд
и ряд 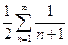 расходится, то абсолютной сходимости нет.
расходится, то абсолютной сходимости нет.