IV этап. Постановка домашнего задания.
1) Выучите доказательство формулы Герона одним из двух способов. 2) Докажите формулу Брахмагупты [2]: площадь четырехугольника, вписанного в окружность, вычисляется по формуле: Указание: по свойству четырехугольника, вписанного в окружность, сумма его противоположных углов составляет 3) Доказательство формулы Брахмагупты. Дано: Доказать: Объяснение доказательства. Деятельностный подход в объяснении доказательства синтетическим методом с использованием: 1) геометрического конструирования; 2) метода площадей; 3) приема введения вспомогательного отрезка 4) «самого сильного метода в математике». Вспомогательное утверждение (доказывается в 8 классе). Сумма противоположных углов вписанного четырехугольника равна В условиях задачи получаем, что, например, I этап. Геометрическое конструирование. Разобьем четырехугольник II этап. Метод площадей. По формуле Снеллиуса площади треугольника III этап. Тригонометрическое моделирование длины вспомогательного отрезка 1) Прием введения вспомогательного отрезка 2) Приравняем правые части полученных равенств и выразим 3) IV этап, заключительный. Подставив это выражение в формулу площади четырехугольника, возведенную в квадрат, и четырежды применяя «самый сильный метод в математике», получим: Отсюда получаем, что
30 (стр. 228, Погорелов). Найдите площадь треугольника по трем сторонам: 2) 5, 5, 6; 3) 17, 65, 80; 5) 13,
|

 , где
, где  - стороны четырехугольника, а
- стороны четырехугольника, а 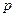 - его полупериметр. (1274, Атанасян).
- его полупериметр. (1274, Атанасян). ; разбить четырехугольник на два треугольника.
; разбить четырехугольник на два треугольника. 30 (2,3,5), 34 (стр. 228, Погорелов).
30 (2,3,5), 34 (стр. 228, Погорелов). - четырехугольник, описанная окружность,
- четырехугольник, описанная окружность,  ,
,  .
. , где
, где  .
. ;
; .
.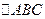 и
и  диагональю
диагональю 
 .
. через стороны четырехугольника, пользуясь теоремой косинусов и основным тригонометрическим тождеством:
через стороны четырехугольника, пользуясь теоремой косинусов и основным тригонометрическим тождеством:
 ; в
; в 
 ;
;

 ;
;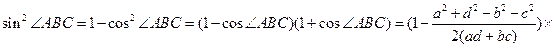
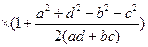 .
.


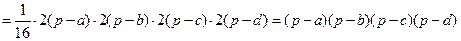
 . Ч.т.д.
. Ч.т.д. .
.


