II этап. Введение нового материала.
Объяснить доказательство формулы Герона двумя способами: 1) методом алгебраического моделирования с использованием синтетического метода и 2) аналитико-синтетическим методом с использованием тригонометрических знаний. 0 этап. Теорема. Площадь треугольника, стороны которого равны Опорная задача-теорема. Во всяком треугольнике хотя бы два угла острые.
Дано:
Доказать: Объяснение доказательства. 1-ый способ доказательства: 1) синтетическим методом; 2) методом опорных задач-теорем; 3) методом геометрического конструирования; 4) методом алгебраического моделирования; 5) с использованием «самого сильного метода в математике»; 6) методом разложения на множители по формуле 7) методом площадей по формуле I этап. Геометрическое конструирование (моделирование). Пусть в исходном II этап. Алгебраическое моделирование на основе двукратного применения теоремы Пифагора. 1) Введем неизвестные величины: 2) По теореме Пифагора, примененной дважды к двум прямоугольным треугольникам, получим: а) в б) в 3) Получаем систему трех уравнений с тремя неизвестными
4) Работа с математической моделью (по А.Г.Мордковичу). Решим эту систему относительно
(деление на 5) Метод разложений на множители в выражении для а) Преобразуем полученное выражение для
б) Трижды используя «самый сильный метод в математике», получим:
в) Значит,
Отметим, что 6) Метод площадей. По основной формуле площади треугольника
2-ой способ доказательства аналитико-синтетическим методом с использованием тригонометрических знаний.
II этап. Из теоремы косинусов и основного тригонометрического тождества получим: 1) 2)
Отметим, что по условию III этап. Трехкратное применение «самого сильного метода в математике». Тогда (прием: самый сильный метод в математике, по М.А.Красносельскому, - «добавить» и «отнять» одно и то же выражение):
IV этап, заключительный. 1) Имеем: 2) Поскольку 3) Подставим полученное выражение в известную формулу для площади, получим:
|

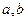 и
и 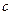 , вычисляется по формуле
, вычисляется по формуле 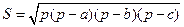 , где
, где 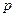 - полупериметр.
- полупериметр.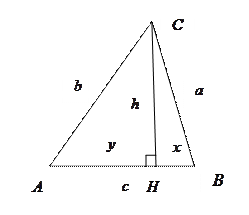 Объяснение доказательства (методом от противного). Предположим, что существует треугольник
Объяснение доказательства (методом от противного). Предположим, что существует треугольник  , в котором два угла тупые:
, в котором два угла тупые:  и
и  . Тогда
. Тогда  (поскольку
(поскольку 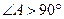 и
и 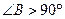 ). Но, по теореме о сумме углов треугольника,
). Но, по теореме о сумме углов треугольника, 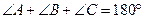 . Получаем противоречие:
. Получаем противоречие:  , т.е.
, т.е. 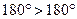 . Значит, наше предположение неверно и в каждом треугольнике хотя бы два угла острые, ч.т.д.
. Значит, наше предположение неверно и в каждом треугольнике хотя бы два угла острые, ч.т.д.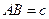 ,
, 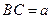 ,
,  ,
,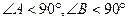 .
.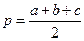 .
.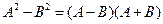 ;
; .
.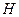 лежит между
лежит между 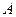 и
и 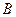 (вершинами двух острых углов) (задача № 35, стр. 64, Погорелов). Из точки
(вершинами двух острых углов) (задача № 35, стр. 64, Погорелов). Из точки 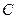 проведем высоту
проведем высоту 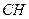 . Тогда ее основание
. Тогда ее основание 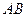 на две части.
на две части.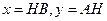 и
и 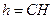 ; очевидно, что
; очевидно, что  .
.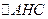

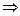
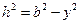 ;
;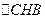
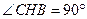
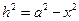 .
. (и тремя параметрами
(и тремя параметрами 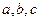 ):
):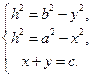 - это алгебраическая модель геометрической ситуации.
- это алгебраическая модель геометрической ситуации.

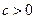 ).
). .
.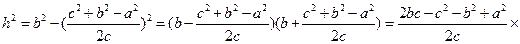
 Отметим, что по условию
Отметим, что по условию 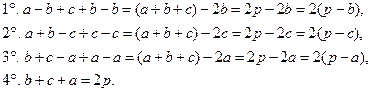
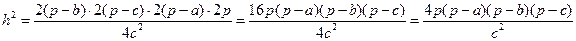 и, следовательно,
и, следовательно, 
 и
и 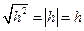 , поскольку
, поскольку  .
. . Тогда, подставив в эту формулу найденное выражение для
. Тогда, подставив в эту формулу найденное выражение для  , получим:
, получим: . Ч.т.д.
. Ч.т.д.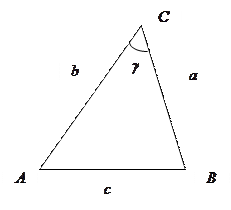 I этап. Восходящий анализ. Имеем:
I этап. Восходящий анализ. Имеем:  , где
, где 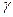 есть угол, лежащий против стороны
есть угол, лежащий против стороны 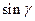 через стороны треугольника.
через стороны треугольника.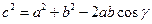
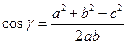

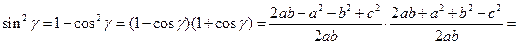
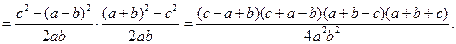
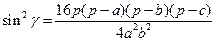
 и
и 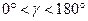 , то
, то  и
и 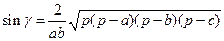
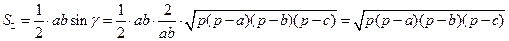 . Ч.т.д.
. Ч.т.д.


