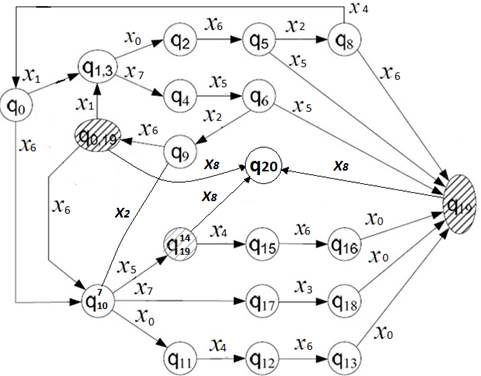
Исходный автомат
Цель работы
Разбиение множества состояний автомата на классы эквивалентности с помощью алгоритма Мили.
Таблица переходов
Граф переходов
Текст программы разбиения состояний на эквивалентные пары #include "stdafx.h" #include <iostream>
const int N=21; //число строк в таблице переходов M int F[N+1][N+1]; //матрица первоначального разбиения на классы int MP[25][25]; //матрица пар int NMP; //число строк в матрице пар NMP const int M[N+1][9]= {{21,2,21,21,21,21,8,21,20}, {3,21,21,21,21,21,21,4,21}, {21,21,21,21,21,5,21,21}, {21,21,8,21,21,18,21,21,21}, {21,21,9,21,21,18,21,21,21}, {10,21,9,21,21,13,21,16,21}, {21,21,21,21,0,21,18,21,21}, {21,21,21,21,21,21,1,21,21}, {21,21,21,21,11,21,21,21,21}, {21,21,21,21,21,21,12,21,21}, {18,21,21,21,21,21,21,21,21}, {21,21,21,21,14,21,21,21,19}, {21,21,21,21,21,21,15,21,21}, {18,21,21,21,21,21,21,21,21}, {21,21,21,17,21,21,21,21,21}, {18,21,21,21,21,21,21,21,21}, {21,21,21,21,21,21,21,21,19}}; //построение матрицы F первоначального разбиения на классы void doF() { int G[N+1]; //вектор, для фиксирования состояний, //которые уже включены в какой-то класс for (int i = 1; i <= N; i++) //инициализация вектора G G[i] = 0; for (int i = 1; i <= N; i++) { if (G[i] == 0) { F[i][i] = i; for (int k = i + 1; k <= N; k++) { if (G[k] == 0) { int j = -1; do{j++;} while (!((j == 8) || (M[i][j] == 22) && (M[k][j]!= 22) || (M[k][j] == 22) && (M[i][j]!= 22))); if(j == 8){F[i][k] = i;G[k] = 1;} else{F[i][k] = 0; } } } } else { for(int s = i; s <= N; s++) F[i][s] = 0; } } }
//построение марицы пар MP void doMP() { int GF[N+1]; //вектор, хранящий номера состояний, уже включенных в //один класс с состоянием i int t = 0; for (int i = 1; i <= N; i++) { for (int s = 1; s <=N; s++) GF[s] = 0; int j = 0; for (int k = i; k <=N; k++) { if (F[i][k]!= 0) { j++; GF[j] = k; } } if (j >= 2) { for (int l = j; l >= 2; l--) { for (int m = l - 1; m >= 1; m--) { MP[t][0] = 0; MP[t][1] = GF[m]; MP[t][2] = GF[l]; for (int k = 0; k <= 8; k++) { MP[t][3+2*k] = M[GF[m]][k]; MP[t][4+2*k] = M[GF[l]][k]; } t++; } } } } NMP = t; }
void doMP2() { int smp = 0, smps = 0; do { smps = smp; smp = 0; for (int i = 0; i < NMP; i++) { int k = -1; do { k++; if (MP[i][3+2*k]!= MP[i][4+2*k]) { int pr = 1; int t = 0; do { t++; if (MP[t-1][0] == 0) { if ((MP[i][3+2*k] == MP[t-1][1] || MP[i][3+2*k] == MP[t-1][2]) &&(MP[i][4+2*k] == MP[t-1][1] || MP[i][4+2*k] == MP[t-1][2])) { pr = 0; } } } while(!(t == NMP || pr == 0)); MP[i][0] = pr; } } while(!(k == 8 || MP[i][0] == 1)); smp = smp + MP[i][0]; } } while(smp!= smps); for (int i = 0; i < NMP; i++) { if (MP[i][0] == 0) { std::cout << MP[i][1] << " " << MP[i][2] << "\n"; } } }
int main() { doF(); doMP(); std::cout << "Eqivalent pairs:\n"; doMP2(); return 0; }
Результаты работы программы эквивалентные пары: 12 15 13 16 13 18 16 18
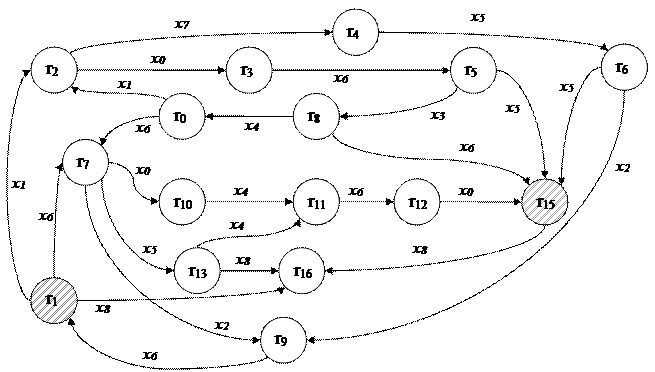
Таблица минизации автомата Полученные пары состояний образуют два класса эквивалентности: {q12, q15}, {q13, q16, q18}. Все другие состояния, не вошедшие в эти классы эквивалентности, эквивалентны сами себе и образуют индивидуальные классы. В нашем примере к перечисленным двум классам эквивалентности следует добавить еще 16 классов: {q0}, {q0,19}, {q1,3},{q2}, {q4}, {q5}, {q6}, {q7,10}, {q8}, {q9}, {q11}, {q14,19}, {q17}, {q19}, {q20}, {q21}. Поставим в соответствие классам эквивалентности состояния минимального автомата (rn): r0 = {q0}, r1 = {q0,19}, r2 = {q1,3}, r3 = {q2}, r4 = {q4}, r5 = {q5}, r6 = {q6}, r7 = {q7,10}, r8 = {q8}, r9 = {q9}, r10 = {q11}, r11 = {q12, q15}, r12 = {q13, q16, q18}, r13 = {q14,19}, r14 = {q17}, r15 = {q19}, r16 = {q20}, r17 = {q21}. r17 – состояние «Ошибка».
|