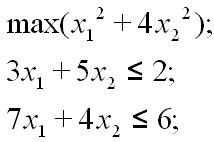ЖАЛПЫ БӨЛІМ

№ п/п	Зміст господарських операцій	Кореспонденція рахунків
Дебет	Кредит
	Отримання розмінної готівки з головної каси в операційну
	Надходження готівки з банку
	Погашення готівкою короткостроковий вексель
	Погашення дебіторської заборгованості покупцем продукції, товарів, робіт, послуг
	Отримані кошти: від винних осіб за завдані збитки від підзвітних осіб (залишок авансу)	30, 331
	Отриманобезповоротну фінансову допомогу
	Перепродані власні акції
	Отримано цільове фінансування
	Повернено зайво видану заробітну плату
	Одержана виручка при роздрібній торгівлі
	Отримано дохід від реалізації необоротніх активів
	Отримано надзвичайні доходи
	Отримано кошти за надані послуги		703/2
	Передано готівку на рахунок в банку
	Передано готівку інкасатору, відправлено через поштове відділення для наступного зарахування на рахунок банку
	Зарахування готівки, внесеної інкасатором, відправленої через поштове відділення, на рахунок банку
	Видано готівку під звіт
	Погашено заборгованість перед: Пенсійним фондом; фондом соціального страхування; фондом безробіття; фондом страхування від нещасних випадків.
	Виплачено заробітню плату
	Виплачені девіденди

 

1 (1).

Запитання:

Цільовою функцією задачі: є функція:

2 (2).

Запитання:

Цільовою функцією задачі: є функція:

Тема: "Досл.опер-Постановка задач багатокритеріальної оптимізації" (2)

 

1 (3).

Запитання:

Серед перерахованих задач вказати задачі багатокритеріальні:

2 (4).

Запитання:

Серед перерахованих задач вказати задачі однокритеріальні:

Тема: "Досл.опер-Заміна обладнання тривалого використання" (2)

 

1 (5).

Запитання:

Замінювати обладнання треба:

2 (6).

Запитання:

Замінювати обладнання треба:

Тема: "Досл.опер-Динамічна модель заміни обладнання" (2)

 

1 (7).

Запитання:

Вартість автомобіля $10000. Через 5 років його можна продати за половину вартості. Можна взяти цей автомобіль у лізінг з сплатою по роках 700, 800,1000, 1100, 1200 дол. Що вигідніше? Часову вартість грошей не враховувати.

2 (8).

Запитання:

Вартість комбайна $50000. Через 5 років його можна продати за половину вартості. Можна взяти цей комбайн у лізінг з сплатою по роках 3500, 4000,5000, 6000, 6500 дол. Що вигідніше? Часову вартість грошей не враховувати.

Тема: "Досл.опер-Календарний графік" (2)

 

1 (9).

Запитання:

Вільний резерв некритичної операції:

2 (10).

Запитання:

Календарні терміни некритичної операції можна:

Тема: "Досл.опер-Сітьова модель" (2)

 

1 (11).

Запитання:

Критичний шлях у сіті програми відображає:

2 (12).

Запитання:

Сітьова модель може мати:

Тема: "Досл.опер-Однопродуктова модель управління запасами" (2)

 

1 (13).

Запитання:

Нехай К – витрати на оформлення замовлення, h – витрати на зберігання одиниці запасу, B(beta) – інтенсивність попиту. Тоді, згідно формули Уілсона, оптимальний розмір замовлення y* дорівнює:

2 (14).

Запитання:

Нехай К – витрати на оформлення замовлення, h – витрати на зберігання одиниці запасу, B(beta) – інтенсивність попиту. Тоді, згідно формули Уілсона, оптимальна тривалість цикла замовлення t* дорівнює:

Тема: "Досл.опер-Параметри і характеристики задач управління запасами" (2)

 

1 (15).

Запитання:

ДЕКІЛЬКА ПРАВИЛЬНИХ ВІДПОВІДЕЙ. В задачах управління запасами шуканими є величини:

2 (16).

Запитання:

В задачах управління запасами заданими є величини:

Тема: "Досл.опер-Розв'язок гри у чистих стратегіях" (2)

 

1 (17).

Запитання:

Чи має гра з матрицею розв'язок у чистих стратегіях?

2 (18).

Запитання:

Розв'язати гру з платіжною матрицею у чистих стратегіях і вказати число -- ціну гри. (Відповідь ввести цифрою)

Тема: "Досл.опер-Розв'язок гри у мішаних стратегіях" (2)

 

1 (19).

Запитання:

Чи має гра з матрицею розв'язок у мішаних стратегіях?

2 (20).

Запитання:

Чи має гра з матрицею розв'язок у мішаних стратегіях?

Тема: "Досл.опер-Парна гра з нульовою сумою" (2)

 

1 (21).

Запитання:

Знайти верхню ціну гри з платіжною матрицею (Відповідь ввести цифрою)

2 (22).

Запитання:

Знайти нижню ціну гри з платіжною матрицею (Відповідь ввести цифрою)

Тема: "Досл.опер-Методи розв'язання багатокритеріальних задач" (2)

 

1 (23).

Запитання:

При розв'язанні багатокритеріальних задачі:

2 (24).

Запитання:

При розв'язанні однокритеріальних задач:

Тема: "Досл.опер-Схема застосування динамічного програмування." (2)

 

1 (25).

Запитання:

Метод динамічного програмування застосовується для задач з (вказати вірні твердження):

2 (26).

Запитання:

Метод динамічного програмування застосовується для задач з (вказати вірні твердження):

Тема: "Досл.опер-Методи дослідження операцій" (3)

 

1 (27).

Запитання:

Досліджується робота станції по ремонту автомобілів. Краще застосувати:

2 (28).

Запитання:

Шукається найдешевший поживний раціон харчування птахів. Краще застосувати:

3 (29).

Запитання:

ОДНА ПРАВИЛЬНА ВІДПОВІДЬ. Досліджується задача оптимального набору висоти літаком. Краще застосувати:

Тема: "Досл.опер-Параметри і складові частини СМО" (2)

 

1 (30).

Запитання:

Які з перерахованих нижче понять є параметрами СМО?

2 (31).

Запитання:

Які з перерахованих нижче понять є складовими частинами СМО?

Тема: "Досл.опер-Характеристики СМО" (2)

 

1 (32).

Запитання:

Які з перерахованих нижче понять є характеристиками роботи СМО з очікуванням?

2 (33).

Запитання:

Які з перерахованих нижче понять є характеристиками роботи СМО з відмовами?

Тема: "Досл.опер-Класифікація СМО" (3)

 

1 (34).

Запитання:

Досліджується робота регістратури поліклініки, яка має 3 регістратора. Треба застосувати модель:

2 (35).

Запитання:

Досліджується робота авіадиспетчерів по управлінню приземленням літаків. Треба застосувати модель:

3 (36).

Запитання:

Досліджується робота телефонного комутатора ін-ту КРОК. Треба застосувати модель:

Тема: "Досл.опер-Найпростіший потік вимог СМО" (2)

 

1 (37).

Запитання:

Які з перелічених нижче характеристик властиві найпростішому потоку?

2 (38).

Запитання:

Які з перелічених нижче характеристик властиві найпростішому потоку?

Тема: "Досл.опер-Показниковий закон обслуговування вимог у СМО" (2)

 

1 (39).

Запитання:

Якщо час обслуговування вимоги розподілений за показниковим законом з інтенсивністю µ, то середній час обслуговування дорівнює:

2 (40).

Запитання:

Якщо час обслуговування вимоги розподілений за показниковим законом з середнім Т, то інтенсивність потоку обслужених каналом вимог дорівнює:

Тема: "Досл.опер-Граф СМО" (2)

 

1 (41).

Запитання:

За графом СМО система рівнянь для стаціонарних ймовірностей станів має вигляд:

2 (42).

Запитання:

За графом СМО система рівнянь для стаціонарних ймовірностей станів має вигляд:

Тема: "Досл.опер-Розв'язок ігор 2n, m2" (2)

 

1 (43).

Запитання:

Розв'язати гру з матрицею у мішаних стратегіях, вказати число -- ціну гри.

2 (44).

Запитання:

Розв'язати гру з матрицею у мішаних стратегіях, вказати число -- ціну гри.

Тема: "Досл.опер-Спрощення гри домінуючими стратегіями" (2)

 

1 (45).

Запитання:

З використанням домінування стратегій гра з матрицею зводиться до гри з матрицею:

2 (46).

Запитання:

З використанням домінування стратегій гра з матрицею зводиться до гри з матрицею:

Тема: "Досл.опер-Зведення гри до задачі лінійного програмування" (2)

 

1 (47).

Запитання:

Гра з матрицею з точки зору одного з гравців зводиться до такої задачі лінійного програмування:

2 (48).

Запитання:

Гра з матрицею з точки зору одного з гравців зводиться до такої задачі лінійного програмування:

Тема: "Досл.опер-Задача про найкоротший шлях" (2)

 

1 (49).

Запитання:

Методом динамічного програмування знайдіть довжину найкоротшого шляху від точки А до точки В на такій схемі доріг (рухатись можна вправо і вгору): Довжина доріг у кілометрах позначена на схемі. (Відповідь ввести числом)

2 (50).

Запитання:

Методом динамічного програмування знайдіть довжину найкоротшого шляху від точки А до точки В на такій схемі доріг (рухатись можна вправо і вгору): Довжина доріг у кілометрах позначена на схемі. (Відповідь ввести числом)

ЖАЛПЫ БӨЛІМ