АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ Прямаянаплоскости 1) Выписать нормальный вектор а) 5х-2у+7=0 б) 4х+9у=0 в) 5у+1=0 г) 3х+8=0 д) у=2 е) х=-3
2) Составить уравнения прямых, проходящих через данную точку М0 перпендикулярно данному вектору а) М0(2,-3) д) М0(1,4)
3) Составить уравнения прямых, проходящих через данную точку М0 параллельно данному вектору а) М0(1,-5)
4) Составить уравнения прямых, проходящих через две данные точки М1 и М2 а) М1(2,-7) М2(3,4); б) М1(1,-3) М2(5,-1); в) М1(1,8) М2(2,-7) г) М1(1,3) М2(1,-4); д) М1(3,-2) М2(5,-2); е) М1(2,7) М2(2,-1)
5) Составить уравнения прямых, отсекающих на осях координат отрезки а) а=2, в=-3 б) а=5, в=1 в) а=3, в=-4
6) Вычислить площадь треугольника, отсекаемого прямой l от координатного угла а) 3х-2у+6=0 б)-2х+у-4=0 в) х-5у-10=0
7) Рассмотреть пары прямых, выявить параллельные, перпендикулярные, найти угол между прямыми а) х-2у+7=0 (l1) б) 3х-6у+1=0 (l1) в) 2х-8у+5=0 (l1) г) х-8у+1=0 (l1) 2х-4у+1=0 (l2) 6х+3у-7=0 (l2) -х+4у+3=0 (l2) 8х+у-5=0 (l2) д) 3х-у+5=0 (l1) е) х-5у+1=0 (l1) 2х+у-7=0 (l2) 2х+3у-7=0 (l2)
8) При каком значении а) 2х-3у+5=0 l1 б) х -
9) При каком а)
10) Составить уравнение прямой l1, проходящей через данную точку М0 параллельно данной прямой l а) М0(5,-2) l: 3х-у=0 б) М0(1,0) l: х-2у+1=0 в) М0(1,-3) l: х-5у+2=0 г) М0(0,-3) l: х-6у=0
11) Составить уравнение прямой l1, проходящей через точку М0 перпендикулярно прямой l а) М0(2,-4) l: х+3у-2=0 б) М0(1,0) l: х-у+7=0 в) М0(1,-8) l: 3х+5=0 г) М0(2,0) l: 5у+2=0
12) Вычислить расстояние от точки М0 до прямой l а) М0(2,-7) l:х-2у+3=0 б) М0(2,-3) l:3у+7=0 в) М0(1,-2) l:2х+5=0
14) Даны вершины 16) Вычислить расстояние между параллельными прямыми а) l1: 3х-4у-10=0 б) l1:х-2у+1=0 в) l1:2х+у-7=0 l2: 6х-8у+5=0 l2:2х-4у+5=0 l2:4х+2у-1=0
17) Найти проекцию точки Р на прямую l а) Р(-6,4) l:4х-5у+3=0 б) Р(1,0) l:х+2у-5=0
18) Найти точки пересечения прямых а) х+5у-1=0 б) 3х-у+1=0 в) 2х+3у-5=0 2х-7у+4=0 х-2у+2=0 3х-5у+3=0
Плоскость 1)Составить уравнение плоскости, проходящей через точку М0 а) М0 (2,-1,3)
2)Выписать нормальные вектора плоскостей а) 3x-5y+2z-7=0 б) 5y-x+11=0 в) x-y+2z=0 г) 2y+z=0 д) x=-2 е) y=5 ж) z-3=0
1) Составить уравнение плоскости, проходящие через 3 данные точки М1, М2 и М3 а) М1 (1,2,-3) М2 (2,-1,0) М3 (1,5,2) б) М1 (5,-4,1) М2 (3,0,-2) М3 (1,2,1)
2) Составить уравнение плоскости, отсекающей на всех координат отрезки a,b,c. Построить плоскости а) a=5, b=2, c=-4 б) a=-2, b=2, c=1 в) a=3, b=-2, c=5
3) Построить плоскости и вычислить площади треугольников, которые эти плоскости отсекают от координатных углов. а) x+2y+3z-6=0 б) 2x-5y+z+10=0 в) 3x-5y+z-15=0
4) При каких значениях l и m плоскости параллельны? 926(1) 2x+ly+3z-5=0 mx-6y-6z+z=0
5) При каком l плоскости перпендикулярны? 927(1) 3x-5y+lz-3=0 x+3y+2z+5=0
8) Найти угол между плоскостями. 928 а) x-y в) 6x+3y-2z=0, x+2y+6z-12=0; г) x+2y+2z-3=0, 16x+12y-15z-1=0
10) Составить уравнения плоскостей, проходящих через а) точку М1(2,-3,5) параллельную плоскости oxy, б) точку М1(1,-5,1) параллельную плоскости oxz, в) точку М1(0,-1,2) параллельную плоскости oyz.
11) Составить уравнение плоскости а) М0 (5,1,-2) б) М0 (1,-2,1)
11)Вычислить расстояние от точки М0 до плоскости а) М0(2,3,-5) б) М0(1,0,1)
Прямая в пространстве
1. Составить канонические и параметрические уравнения прямых а) проходящей через точку М0(2,-1,3) параллельно вектору б) проходящей через точку М0(2,-3,1) параллельно вектору в) проходящей через две точки М1(5,-2,1) и М2(1,-3,4) г)
2. Выписать направляющий вектор прямой а) 3. Доказать параллельность прямых а) б) 4. Доказать перпендикулярность прямых а) б) 5. Найти угол между прямыми а) б)
в)
Прямая и плоскость в пространстве
1. Найти точку пересечения прямой и плоскости а) б) 2. При каком значении m прямая параллельна плоскости а) б) 3. При каких значениях А и В прямая перпендикулярна плоскости а) б) 4. Найти угол между прямой и плоскостью а) б) 5. Составить уравнение плоскости, проходящей через точку М(3,5,-4) перпендикулярно прямой 6. Составить уравнение перпендикуляра, опущенного из точки К(2,-1,3) на плоскость 3x-2y+z-5=0. 7.Найти проекцию точки А(2,-1,0) на плоскость x-2y+z-2=0
|

 и угловой коэффициент k прямых, построить прямые
и угловой коэффициент k прямых, построить прямые
 прямые параллельные?
прямые параллельные? . А(1,1) В(3,3) С(5,2) найти: 1) уравнение и длину стороны АС, 2) уравнение и длину медианы ВМ, 3) уравнение и длину высоты ВК, 4)
. А(1,1) В(3,3) С(5,2) найти: 1) уравнение и длину стороны АС, 2) уравнение и длину медианы ВМ, 3) уравнение и длину высоты ВК, 4) 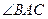 , 5) уравнение прямой, проходящей через точку В параллельную АС.
, 5) уравнение прямой, проходящей через точку В параллельную АС. вектору
вектору 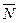
 +z-1=0, x+y
+z-1=0, x+y 


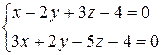 д)
д) 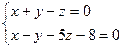
 б)
б)  в)
в)  г)
г) 

 и
и 
 и
и 

 и
и 
 и
и 
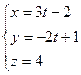 г)
г)  и
и 












 и 2x-y+z+3=0
и 2x-y+z+3=0