Задача № 6.
Определить компланарны ли вектора  , , 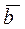 и и  . .
| № п/п
| 
| 
| 
| | 6.1
| (2, 3,1)
| (-1, 0, -1)
| (2, 2, 2)
| | 6.2
| (3, 2, 1)
| (2, 3, 4)
| (3, 1, -1)
| | 6.3
| (1, 5, 2)
| (-1, 1, -1)
| (1, 1, 1)
| | 6.4
| (1, -1, -3)
| (3, 2, 1)
| (2, 3, 4)
| | 6.5
| (3, 3, 1)
| (1, -2, 1)
| (1, 1, 1)
| | 6.6
| (3, 1, -1)
| (-2, -1, 0)
| (5, 2, -1)
| | 6.7
| (4, 3, 1)
| (1, -2, 1)
| (2, 2, 2)
| | 6.8
| (4, 3, 1)
| (6, 7, 4)
| (2, 0, -1)
| | 6.9
| (3, 2, 1)
| (1, -3, -7)
| (1, 2, 3)
| | 6.10
| (3, 7, 2)
| (-2, 0, -1)
| (2, 2, 1)
| | 6.11
| (1, -2, 6)
| (1, 0, 1)
| (2, -6, 17)
| | 6.12
| (6, 3, 4)
| (-1, -2, -1)
| (2, 1, 2)
| | 6.13
| (7, 3, 4)
| (-1, -2, -1)
| (4, 2, 4)
| | 6.14
| (2, 3, 2)
| (4, 7, 5)
| (2, 0, -1)
| | 6.15
| (5, 3, 4)
| (-1, 0, -1)
| (4, 2, 4)
| | 6.16
| (3, 10, 5)
| (-3, -2, -3)
| (2, 4, 3)
| | 6.17
| (-2, -4, -3)
| (4, 3, 1)
| (6, 7, 4)
| | 6.18
| (3, 1, -1)
| (1, 0, -1)
| (8, 3, -2)
| | 6.19
| (4, 2, 2)
| (-3, -3, -3)
| (2, 1, 2)
| | 6.20
| (4, 1, 2)
| (9, 2, 5)
| (1, 1, -1)
| | 6.21
| (5, 3, 4)
| (4, 3, 3)
| (9, 5, 8)
| | 6.22
| (3, 4, 2)
| (1, 1, 0)
| (8, 11, 6)
| | 6.23
| (4, -1, -6)
| (1, -3, -7)
| (2, -1, -4)
| | 6.24
| (3, 1, 0)
| (-5, -4, -5)
| (4, 2, 4)
| | 6.25
| (3, 0, 3)
| (8, 1, 6)
| (1, 1, -1)
| | 6.26
| (1, -1, 4)
| (1, 0, 3)
| (1, -3, 8)
| | 6.27
| (6, 3, 4)
| (-1, -2, -1)
| (2, 1, 2)
| | 6.28
| (4, 1, 1)
| (-9, -4, -9)
| (6, 2, 6)
| | 6.29
| (-3, 3, 3)
| (-4, 7, 6)
| (3, 0, -1)
| | 6.30
| (-7, 10, -5)
| (0, -2, -1)
| (-2, 4, -1)
|
Задача № 7
Вычислить объем пирамиды с вершинами в точках  , , 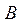 , , 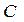 и и
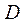 и ее высоту, опущенную из вершины и ее высоту, опущенную из вершины 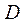 на грань на грань 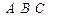 . .
| № п/п
| 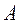
| 
| 
| 
| | 7.1
| (0, 1, 2)
| (2, 1, 7)
| (2, 7, 4)
| (0, 0, 4)
| | 7.2
| (1, 2, 3)
| (2, 8, -4)
| (0, 5, 4)
| (2, 9, 4)
| | 7.3
| (1, 1, 1)
| (2, 4, -2)
| (2, 0, 2)
| (0, 1, -1)
| | 7.4
| (1, -1, 1)
| (0, 2, 3)
| (1, -1, 0)
| (0, 2, 2)
| | 7.5
| (2, 1, 3)
| (4, -2, 0)
| (1, 3, -3)
| (7, 5, 2)
| | 7.6
| (-2, 0, 4)
| (1, 3, -1)
| (4, -1, 3)
| (2, 7, 3)
| | 7.7
| (1, 2, 3)
| (0, 0, 0)
| (1, 4, 3)
| (1, 8, -1)
| | 7.8
| (-1, 2, 0)
| (1, 0, 3)
| (0, 2, 2)
| (1, 8, 3)
| | 7.9
| (2, -1, 1)
| (3, 3, 2)
| (2, 1, 0)
| (4, 1, -3)
| | 7.10
| (2, 1, -1)
| (-3, 1, 2)
| (0, 1, 2)
| (-1, 8, 3)
| | 7.11
| (-2, 1, 1)
| (5, 5, 4)
| (3, 2, -1)
| (4, 1, 3)
| | 7.12
| (0, 1, -1)
| (3, -1, 5)
| (1, 0, 4)
| (3, 5, 7)
| | 7.13
| (1, 1, 2)
| (-1, 1, 3)
| (2, -2, 4)
| (-1, 0, -2)
| | 7.14
| (2, 3, 1)
| (4, 1, -2)
| (6, 3, 7)
| (7, 5, -3)
| | 7.15
| (1, 1, -1)
| (2, 3, 1)
| (3, 2, 1)
| (5, 9, -8)
| | 7.16
| (1, 5, -7)
| (-3, 5, 3)
| (-2, 7, 3)
| (-4, 8, -12)
| | 7.17
| (-3, 4, -7)
| (1, 5, -4)
| (-6, -2, 0)
| (2, 5, 4)
| | 7.18
| (-1, 2, -3)
| (4, -1, 0)
| (2, 1, -2)
| (3, 4, 5)
| | 7.19
| (4, -1, 3)
| (-2, 1, 0)
| (0, -5, 1)
| (3, 2, -6)
| | 7.20
| (1, -1, 1)
| (-2, 0, 3)
| (2, 1, -1)
| (2, -2, -4)
| | 7.21
| (1, 2, 0)
| (1, -1, 2)
| (0, 1, -1)
| (-3, 0, 1)
| | 7.22
| (1, 0, 2)
| (1, 2, -1)
| (2, -2, 1)
| (2, 1, 0)
| | 7.23
| (1, 2, -3)
| (1, 0, 1)
| (-2, -1, 6)
| (0, -5, -4)
| | 7.24
| (3, 10, -1)
| (-2, 3, -5)
| (-6, 0, -3)
| (1, -1, 2)
| | 7.25
| (-1, 2, 4)
| (-1, -2, -4)
| (3, 0, -1)
| (7, -3, 1)
| | 7.26
| (0, -3, 1)
| (-4, 1, 2)
| (2, -1, 5)
| (3, 1, -4)
| | 7.27
| (1, 3, 0)
| (4, -1, 2)
| (3, 0, 1)
| (-4, 3, 5)
| | 7.28
| (-2, -1, -1)
| (0, 3, 2)
| (3, 1, -4)
| (-4, 7, 3)
| | 7.29
| (-3, -5, 6)
| (2, 1, -4)
| (0, -3, -1)
| (-5, 2, -8)
| | 7.30
| (2, -4, -3)
| (5, 6, 0)
| (-1, 3, -3)
| (-10, -8, 7)
|
Рекомендуемая литература
1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры.-М.: Наука, Главная редакция физико-математической литературы, 1984 г.
2. Зимина О.В. Линейная алгебра и аналитическая геометрия. -М.: Издательство МЭИ, 2000 г.
3. Ильин В.А., Позняк Э.Г. Линейная алгебра.- М.: Наука, Главная редакция физико-математической литературы, 1988 г.
4.Данко П.Е.,Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.1.,- М.:Высшая школа, 1986 г.
5. Сборник задач по математике для втузов. Под редакцией Ефимова А.И., Демидовича Б.П.,-М.:Наука, Главная редакция физико-математической литературы, 1986 г.
6. Кузнецов Л.А. Сборник заданий по высшей математике. Типовые расчеты: Учебное пособие.6-е изд., стер.– Спб.: Издательство «Лань», 2005 г.

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|
Тема: Изучение фенотипов местных сортов растений Цель: расширить знания о задачах современной селекции. Оборудование:пакетики семян различных сортов томатов...
Тема: Составление цепи питания Цель: расширить знания о биотических факторах среды. Оборудование:гербарные растения...
В эволюции растений и животных. Цель: выявить ароморфозы и идиоадаптации у растений Цель: выявить ароморфозы и идиоадаптации у растений. Оборудование: гербарные растения, чучела хордовых (рыб, земноводных, птиц, пресмыкающихся, млекопитающих), коллекции насекомых, влажные препараты паразитических червей, мох, хвощ, папоротник...
|
Классификация ИС по признаку структурированности задач Так как основное назначение ИС – автоматизировать информационные процессы для решения определенных задач, то одна из основных классификаций – это классификация ИС по степени структурированности задач...
Внешняя политика России 1894- 1917 гг. Внешнюю политику Николая II и первый период его царствования определяли, по меньшей мере три важных фактора...
Оценка качества Анализ документации. Имеющийся рецепт, паспорт письменного контроля и номер лекарственной формы соответствуют друг другу. Ингредиенты совместимы, расчеты сделаны верно, паспорт письменного контроля выписан верно. Правильность упаковки и оформления....
|
|

 ,
, 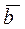 и
и  .
.


 ,
, 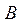 ,
, 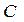 и
и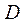 и ее высоту, опущенную из вершины
и ее высоту, опущенную из вершины 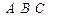 .
.