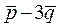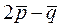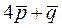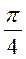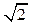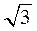Задачи для самостоятельного решения. 1. Определить, какой является тройка (правой или левой),
1. Определить, какой является тройка  (правой или левой), (правой или левой),
если:

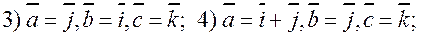
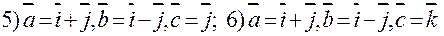
2. Векторы  , образующие правую тройку, взаимно , образующие правую тройку, взаимно
перпендикулярны. Зная, что  , ,  , ,  , ,
вычислить  . .
3. Вектор  перпендикулярен к векторам перпендикулярен к векторам  , угол между , угол между  и и 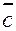
равен 30°. Зная, что  , ,  , ,  , вычислить , вычислить  . .
4. Даны три вектора: 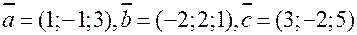
Вычислить  . .
5. Установить, компланарны ли векторы  , если: , если:
1)  ; ;
2)  ; ;
3)  . .
6. Выяснить, является ли система векторов  , линейно , линейно
независимой, если:
1)  ; ;
2)  ; ;
3) 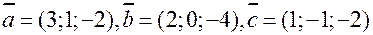 . .
7. Доказать, что четыре точки A(1; 2; – 1), В(0;1;5), С(–1; 2; 1),
D(2; 1; 3)лежат в одной плоскости.
8. Вычислить объем параллелепипеда, построенного на векторах
 . .
9. Вычислить объем тетраэдра, вершины которого находятся в
точках A(2; –1; 3), В(–2;1;4), С(3; –3; 0), D(4; 4; 1).
10. Даны вершины тетраэдра: A(2; 3; 1), В(4;1;–2), С(6; 3; 7), D(–5; –4; 8). Найти длину его высоты, опущенной из вершины D.
11. Объем тетраэдра V = 5, три его вершины находятся в точках A(2; 1; –1), В(3;0;1), С(2; –1; 3) Найти координаты четвертой вершины D, если известно, что она лежит на оси OY.
Варианты индивидуальных заданий
Задача № 1.
Написать разложение вектора  по векторам по векторам 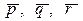 . .
| № п/п
| 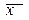
| 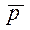
| 
| 
| | 1.1
| (-2, 4, 7)
| (0, 1, 2)
| (1, 0, 1)
| (-1, 2, 4)
| | 1.2
| (6, 12, -1)
| (1, 3, 0)
| (2, -1, 1)
| (0, -1, 2)
| | 1.3
| (1, -4, 4)
| (2, 1, -1)
| (0, 3, 2)
| (1, -1, 1)
| | 1.4
| (-9, 5, 5)
| (4, 1, 1)
| (2, 0, -3)
| (-1, 2, 1)
| | 1.5
| (-5, -5, 5)
| (-2, 0, 1)
| (1, 3, -1)
| (0, 4, 1)
| | 1.6
| (13, 2, 7)
| (5, 1, 0)
| (2, -1, 3)
| (1, 0, -1)
| | 1.7
| (-19, -1, 7)
| (0, 1, 1)
| (-2, 0, 1)
| (3, 1, 0)
| | 1.8
| (3, -3, 4)
| (1, 0, 2)
| (0, 1, 1)
| (2, -1, 4)
| | 1.9
| (2, 2, -1)
| (3, 11, 0)
| (-1, 2, 1)
| (-1, 0, 2)
| | 1.10
| (-1, 7, -4)
| (-1, 2, 1)
| (2, 0, 3)
| (1, 1, -1)
| | 1.11
| (6, 5, -14)
| (1, 1, 4)
| (0, -3, 2)
| (2, 1, -1)
| | 1.12
| (6, -1, 7)
| (1, -2, 0)
| (-1, 1, 3)
| (1, 0, 4)
| | 1.13
| (5, -15,0)
| (1, 0, 5)
| (-1, 3, 2)
| (0, -1, 1)
| | 1.14
| (2, -1, 11)
| (1, 1, 0)
| (0, 1, -2)
| (1, 0, 8)
| | 1.15
| (11, 5, -3)
| (1, 0, 2)
| (-1, 0, 1)
| (2, 5, -3)
| | 1.16
| (8, 0, 5)
| (2, 0, 1)
| (1, 1, 0)
| (4, 1, 2)
| | 1.17
| (3, 1, 8)
| (0, 1, 3)
| (1, 2, -1)
| (2, 0, -1)
| | 1.18
| (8, 1, 12)
| (1, 2, -1)
| (3, 0, 2)
| (-1, 1, 1)
| | 1.19
| (-9, -8, -3)
| (1, 4, 1)
| (-3, 2, 1)
| (1, -1, 2)
| | 1.20
| (-5, 9, -13)
| (0, 1, -2)
| (3, -1, 1)
| (4, 1, 0)
| | 1.21
| (-15, 5, 6)
| (0, 5, 1)
| (3, 2, -1)
| (-1, 1, 0)
| | 1.22
| (8, 9, 4)
| (1, 0, 1)
| (0, -2, 1)
| (1, 3, 0)
| | 1.23
| (23, -14, -30)
| (2, 1, 0)
| (1, -1, 0)
| (-3, 2, 5)
| | 1.24
| (3, 1, 3)
| (2, 1, 0)
| (1, 0, 1)
| (4, 2, 1)
| | 1.25
| (-1, 7, 0)
| (0, 3, 1)
| (1, -1, 2)
| (2, -1, 0)
| | 1.26
| (11, -1, 4)
| (1, -1, 2)
| (3, 2, 0)
| (-1, 1, 0)
| | 1.27
| (-13, 2, 18)
| (1, 1, 4)
| (-3, 0, 2)
| (1, 2, -1)
| | 1.28
| (0, -8, 9)
| (0, -2, 1)
| (3, 1, -1)
| (4, 0, 1)
| | 1.29
| (8, -7, -13)
| (0, 1, 5)
| (3, -1, 2)
| (-1, 0, 1)
| | 1.30
| (2, 7, 5)
| (1, 0, 1)
| (1, -2, 0)
| (0, 3, 1)
|
Задача № 2.
Определить коллинеарны ли векторы 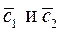 , построенные на , построенные на
векторах  . .
| № п/п
| 
| 
| 
| 
| | 2.1
| (1, -2, 3)
| (3, 0, -1)
| 
| 
| | 2.2
| (1, 0, -1)
| (-2, 3, 5)
| 
| 
| | 2.3
| (-2, 4, 1)
| (1, -2, 7)
| 
| 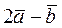
| | 2.4
| (1, 2, -3)
| (2, -1, -1)
| 
| 
| | 2.5
| (3, 5, 4)
| (5, 9, 7)
| 
| 
| | 2.6
| (1, 4, -2)
| (1, 1, -1)
| 
| 
| | 2.7
| (1, -2, 5)
| (3, -1, 0)
| 
| 
| | 2.8
| (3, 4, -1)
| (2, -1, 1)
| 
| 
| | 2.9
| (2, -3, -2)
| (1, 0, 5)
| 
| 
| | 2.10
| (-1, 4, 2)
| (3, -2, 6)
| 
| 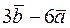
| | 2.11
| (5, 0, -1)
| (7, 2, 3)
| 
| 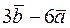
| | 2.12
| (0, 3, -2)
| (1, -2, 1)
| 
| 
| | 2.13
| (-2, 7, -1)
| (-3, 5, 2)
| 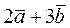
| 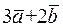
| | 2.14
| (3, 7, 0)
| (1, -3, 4)
| 
| 
| | 2.15
| (-1, 2, -1)
| (2, -7, 1)
| 
| 
| | 2.16
| (7, 9, -2)
| (5, 4, 3)
| 
| 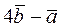
| | 2.17
| (5, 0, -2)
| (6, 4, 3)
| 
| 
| | 2.18
| (8, 3, -1)
| (4, 1, 3)
| 
| 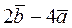
| | 2.19
| (3, -1, 6)
| (5, 7, 10)
| 
| 
| | 2.20
| (1, -2, 4)
| (7, 3, 5)
| 
| 
| | 2.21
| (3, 7, 0)
| (4, 6, -1)
| 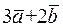
| 
| | 2.22
| (2, -1, 4)
| (3, -7, -6)
| 
| 
| | 2.23
| (5, -1, -2)
| (6, 0, 7)
| 
| 
| | 2.24
| (-9, 5, 3)
| (7, 1, -2)
| 
| 
| | 2.25
| (4, 2, 9)
| (0, -1, 3)
| 
| 
| | 2.26
| (2, -1, 6)
| (-1, 3, 8)
| 
| 
| | 2.27
| (5, 0, 8)
| (-3, 1, 7)
| 
| 
| | 2.28
| (-1, 3, 4)
| (2, -1, 0)
| 
| 
| | 2.29
| (4, 2, -7)
| (5, 0, -3)
| 
| 
| | 2.30
| (2, 0, -5)
| (1, -3, 4)
| 
| 
|
Задача № 3
Найти косинус угла между векторами  . .
| № п/п
| 
| 
| 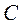
| | 3.1
| (6, 5, 1)
| (0, 1, 2)
| (2, 1, 0)
| | 3.2
| (5, 4, 2)
| (1, 2, 3)
| (3, 2, 1)
| | 3.3
| (2, 0, 4)
| (1, 1, 1)
| (3, 2, 1)
| | 3.4
| (1, 2, 3)
| (2, -1, 0)
| (3, 2, 1)
| | 3.5
| (1, -1, 2)
| (5, -6, 2)
| (2, 3, -1)
| | 3.6
| (3, -3, 1)
| (-3, -2, 0)
| (5, 0, 2)
| | 3.7
| (4, 2, 1)
| (0, 4, 5)
| (1, 2, 7)
| | 3.8
| (1, 0, 2)
| (2, 4, 3)
| (1, 7, 1)
| | 3.9
| (5, -1, 3)
| (2, 0, 1)
| (3, 1, -1)
| | 3.10
| (0, 8, 1)
| (2, 1, 1)
| (-1, 4, 5)
| | 3.11
| (1, 0, 4)
| (0, 2, 3)
| (-1, 1, 0)
| | 3.12
| (2, 3, 4)
| (3, 4, 5)
| (-4, 5, 6)
| | 3.13
| (1, -2, 3)
| (0, -1, 2)
| (3, -4, 5)
| | 3.14
| (0, -3, 6)
| (-12, -3, -3)
| (-9, -3, -6)
| | 3.15
| (3, 3, -1)
| (5, 5, -2)
| (4, 1, 1)
| | 3.16
| (-1, 2, -3)
| (3, 4, -6)
| (1, 1, -1)
| | 3.17
| (-4, -2, 0)
| (-1, -2, 4)
| (3, -2, 1)
| | 3.18
| (5, 3, -1)
| (5, 2, 0)
| (6, 4, -1)
| | 3.19
| (-3, -7, -6)
| (0, -1, -2)
| (2, 3, 0)
| | 3.20
| (2, -4, 6)
| (0, -2, 4)
| (6, -8, 10)
| | 3.21
| (0, 1, -2)
| (3, 1, 2)
| (4, 1, 1)
| | 3.22
| (3, 3, -1)
| (1, 5, -2)
| (4, 1, 1)
| | 3.23
| (2, 1, -1)
| (6, -1, -4)
| (4, 2, 1)
| | 3.24
| (-1, -2, 1)
| (-4, -2, 5)
| (-8, -2, 2)
| | 3.25
| (6, 2, -3)
| (6, 3, -2)
| (7, 3, -3)
| | 3.26
| (0, 0, 4)
| (-3, -6, 1)
| (-5, -10, -1)
| | 3.27
| (2, -8, -1)
| (4, -6, 0)
| (-2, -5, -1)
| | 3.28
| (3, -6, 9)
| (0, 3, 6)
| (9, -12, 15)
| | 3.29
| (0, 2, -4)
| (8, 2, 2)
| (6, 2, 4)
| | 3.30
| (3, 3, -1)
| (5, 1, -2)
| (4, 1, 1)
|
Задача № 4
Определить направляющие косинусы вектора силы  . Найти . Найти
момент силы  , приложенной в точке , приложенной в точке  , относительно точки , относительно точки
 (иначе говоря, найти векторное произведение [ (иначе говоря, найти векторное произведение [  ]). ]).
| № п/п
| 
| 
| 
| | 4.1
| (3, 3, 3)
| (3, -1, 5)
| (4, -2, 3)
| | 4.2
| (4, 4, 4)
| (4, -2, 5)
| (5, -3, 3)
| | 4.3
| (8, -8, 8)
| (10, -8, 1)
| (9, -7, 3)
| | 4.4
| (-2, 2, -2)
| (11, -9, 1)
| (10, -8, 3)
| | 4.5
| (5, 5, 5)
| (5, -3, 5)
| (6, -4, 3)
| | 4.6
| (-3, 3, -3)
| (12, -10, 1)
| (11, -9, 3)
| | 4.7
| (6, 6, 6)
| (6, -4, 5)
| (7, -5, 3)
| | 4.8
| (-4, 4, -4)
| (13, -11, 1)
| (12, -10, 3)
| | 4.9
| (7, 7, 7)
| (7, -5, 5)
| (8, -6, 3)
| | 4.10
| (-5, 5, -5)
| (14, -12, 1)
| (13, -11, 3)
| | 4.11
| (-1, -1, 1)
| (8, -6, -5)
| (9, -7, 3)
| | 4.12
| (3, 3, -3)
| (0, 1, 2)
| (2, -1, -2)
| | 4.13
| (-2, -2, -2)
| (9, -7, 5)
| (10, -8, 3)
| | 4.14
| (4, 4, -4)
| (1, 0, 2)
| (3, 2, -2)
| | 4.15
| (-3, -3, -3)
| (10, -8, 5)
| (11, -9, 3)
| | 4.16
| (5, 5, -5)
| (2, -1, 2)
| (4, -3, 2)
| | 4.17
| (-4, -4, -4)
| (11, -9, 5)
| (12, -10, 3)
| | 4.18
| (6, 6, -6)
| (3, -2, 2)
| (5, -4, -2)
| | 4.19
| (-5, -5, -5)
| (12, -10, 5)
| (13, -11, 3)
| | 4.20
| (7, 7, -7)
| (4, -3, 2)
| (6, -5, -2)
| | 4.21
| (3, -3, 3)
| (5, -3, 1)
| (4, -2, 3)
| | 4.22
| (8, 8, -8)
| (5, -4, 2)
| (7, -6, -2)
| | 4.23
| (4, -4, 4)
| (6, -4, 1)
| (5, -4, 3)
| | 4.24
| (-2, -2, 2)
| (6, -5, 2)
| (8, -7, -2)
| | 4.25
| (5, -5, 5)
| (7, -5, 1)
| (6, -4, 3)
| | 4.26
| (-3, -3, 3)
| (7, -6, 2)
| (9, -8, 2)
| | 4.27
| (6, -6, 6)
| (8, -6, 1)
| (7, -5, 3)
| | 4.28
| (-4, -4, 4)
| (8, -7, 2)
| (10, -9, -2)
| | 4.29
| (7, -7, 7)
| (9, -7, 1)
| (8, -6, 3)
| | 4.30
| (-5, -5, 5)
| (9, -8, 2)
| (11, -10, 2)
|
Задача № 5.
Вычислить площадь параллелограмма, построенного на векторах
 и и  . .
| № п/п
| 
| 
| 
| 
| 
| | 5.1
| 
| 
|
|
| 
| | 5.2
| 
| 
|
|
| 
| | 5.3
| 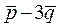
| 
| 
|
| 
| | 5.4
| 
| 
|
| 
| 
| | 5.5
| 
| 
|
|
| 
| | 5.6
| 
| 
|
|
| 
| | 5.7
| 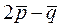
| 
|
|
| 
| | 5.8
| 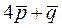
| 
|
|
| 
| | 5.9
| 
| 
|
|
| 
| | 5.10
| 
| 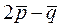
|
|
| 
| | 5.11
| 
| 
|
|
| 
| | 5.12
| 
| 
|
|
| 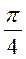
| | 5.13
| 
| 
|
|
| 
| | 5.14
| 
| 
|
|
| 
| | 5.15
| 
| 
|
|
| 
| | 5.16
| 
| 
|
|
| 
| | 5.17
| 
| 
|
|
| 
| | 5.18
| 
| 
|
|
| 
| | 5.19
| 
| 
|
|
| 
| | 5.20
| 
| 
|
|
| 
| | 5.21
| 
| 
|
| 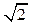
| 
| | 5.22
| 
| 
| 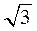
|
| 
| | 5.23
| 
| 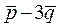
|
|
| 
| | 5.24
| 
| 
| 
|
| 
| | 5.25
| 
| 
|
|
| 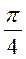
| | 5.26
| 
| 
|
|
| 
| | 5.27
| 
| 
|
| 
| 
| | 5.28
| 
| 
| 2,5
|
| 
| | 5.29
| 
| 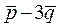
|
|
| 
| | 5.30
| 
| 
|
|
| 
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|
Мелоксикам (Мовалис) Групповая принадлежность
· Нестероидное противовоспалительное средство, преимущественно селективный обратимый ингибитор циклооксигеназы (ЦОГ-2)...
Менадиона натрия бисульфит (Викасол) Групповая принадлежность
•Синтетический аналог витамина K, жирорастворимый, коагулянт...
Разновидности сальников для насосов и правильный уход за ними
Сальники, используемые в насосном оборудовании, служат для герметизации пространства образованного кожухом и рабочим валом, выходящим через корпус наружу...
|
Факторы, влияющие на степень электролитической диссоциации Степень диссоциации зависит от природы электролита и растворителя, концентрации раствора, температуры, присутствия одноименного иона и других факторов...
Йодометрия. Характеристика метода Метод йодометрии основан на ОВ-реакциях, связанных с превращением I2 в ионы I- и обратно...
Броматометрия и бромометрия Броматометрический метод основан на окислении восстановителей броматом калия в кислой среде...
|
|

 (правой или левой),
(правой или левой), 
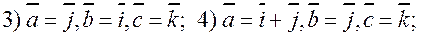
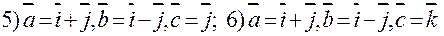
 ,
,  ,
,  ,
, .
. перпендикулярен к векторам
перпендикулярен к векторам  , угол между
, угол между  и
и 
 ,
,  ,
,  , вычислить
, вычислить 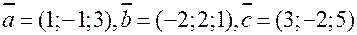
 ;
; ;
; .
. ;
; ;
;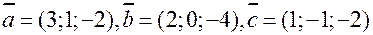 .
. .
. по векторам
по векторам 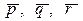 .
.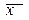
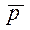


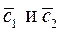 , построенные на
, построенные на .
.








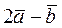












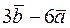


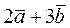
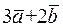



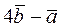


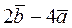










 .
.

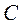
 . Найти
. Найти , приложенной в точке
, приложенной в точке  , относительно точки
, относительно точки (иначе говоря, найти векторное произведение [
(иначе говоря, найти векторное произведение [  ]).
]).


 и
и  .
.