Пусть  – ортонормированный базис,
– ортонормированный базис, 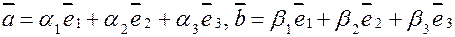 ,
,  - угол между
- угол между  и
и  . Тогда справедливы следующие соотношения:
. Тогда справедливы следующие соотношения:
1. 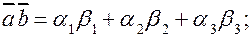
2. 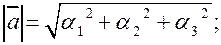
3. 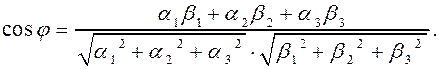
В дальнейшем, если базис явно не указан, будем полагать, что мы пользуемся ортонормированным базисом, векторы которого будем обозначать 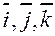 .
.
Ортом ненулевого вектора  называется вектор
называется вектор 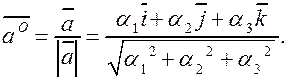
Направляющими косинусами вектора  называются
называются  – косинусы углов, которые образует вектор
– косинусы углов, которые образует вектор  с векторами
с векторами 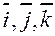 , соответственно. Направляющие косинусы любого вектора
, соответственно. Направляющие косинусы любого вектора  равны координатам его орта
равны координатам его орта
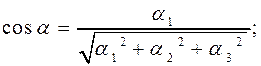
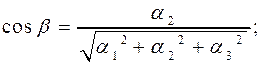
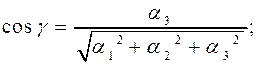
Проекцией вектора  на вектор
на вектор  (обозначается
(обозначается  ) называется число
) называется число  , где
, где  - угол между векторами
- угол между векторами  и
и  .
.
Легко видеть, что если  ,
, 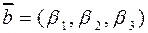 то
то
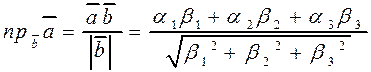
Пример 8. Векторы  и
и  образуют угол
образуют угол  ,
,  Найти
Найти  .
.
Решение. Пользуясь свойствами скалярного произведения, раскрываем скобки и вычисляем каждое из слагаемых, пользуясь определением 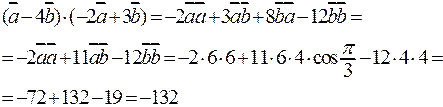
Пример 9. Найти
а) работу силы  при перемещении материальной точки из
при перемещении материальной точки из  в
в  ;
;
б) угол между векторами  и
и  ;
;
в) направляющие косинусы  ;
;
г) проекцию вектора  на
на  .
.
Решение. а) Работа силы  при перемещении материальной точки из
при перемещении материальной точки из  в
в  равна скалярному произведению
равна скалярному произведению  . Находим сначала
. Находим сначала  , а затем
, а затем  .
.
б) 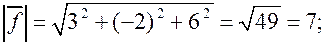
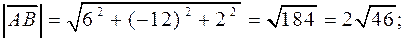
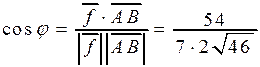
в) Находим орт вектора  :
:
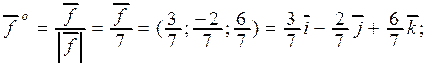
Координаты орта  являются направляющими косинусами вектора
являются направляющими косинусами вектора  . Следовательно,
. Следовательно,
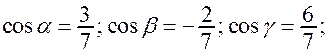
г) Проекция вектора  на
на  равна
равна
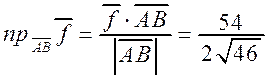
Пример 10. Даны точки  Убедиться, что ABCD является квадратом.
Убедиться, что ABCD является квадратом.
Решение. Найдем векторы сторон. 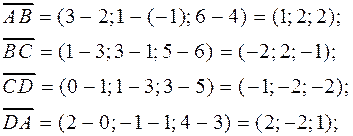
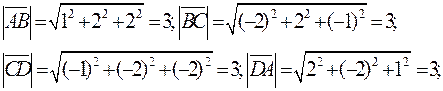 Длины всех сторон равны. Кроме того, векторы
Длины всех сторон равны. Кроме того, векторы 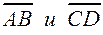
коллинеарны, т.к.  . Следовательно, ABCD является параллелограммом и ромбом (поскольку длины всех сторон равны). Осталось доказать, что
. Следовательно, ABCD является параллелограммом и ромбом (поскольку длины всех сторон равны). Осталось доказать, что 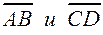 ортогональны. А это следует из того, что
ортогональны. А это следует из того, что 

 – ортонормированный базис,
– ортонормированный базис, 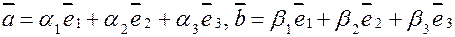 ,
,  - угол между
- угол между  и
и  . Тогда справедливы следующие соотношения:
. Тогда справедливы следующие соотношения: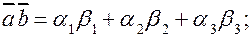
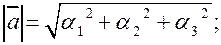
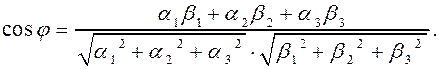
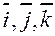 .
. называется вектор
называется вектор 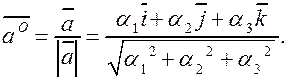
 – косинусы углов, которые образует вектор
– косинусы углов, которые образует вектор 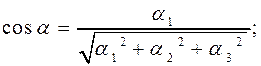
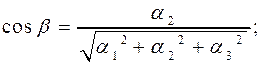
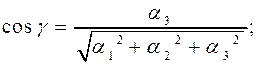
 на вектор
на вектор  (обозначается
(обозначается  ) называется число
) называется число  , где
, где  - угол между векторами
- угол между векторами  ,
, 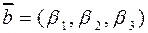 то
то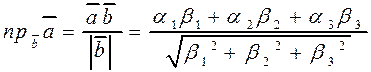
 ,
,  Найти
Найти  .
.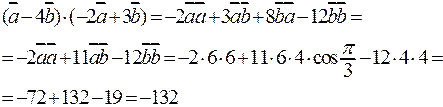
 при перемещении материальной точки из
при перемещении материальной точки из  в
в  ;
; и
и  ;
; . Находим сначала
. Находим сначала  , а затем
, а затем  .
.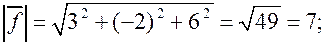
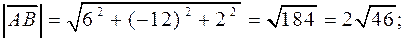
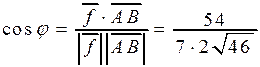
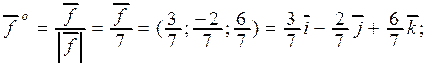
 являются направляющими косинусами вектора
являются направляющими косинусами вектора 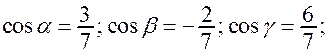
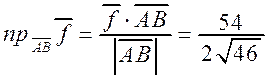
 Убедиться, что ABCD является квадратом.
Убедиться, что ABCD является квадратом.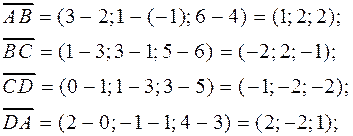
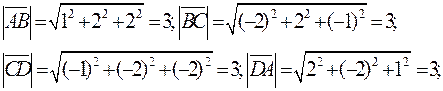 Длины всех сторон равны. Кроме того, векторы
Длины всех сторон равны. Кроме того, векторы 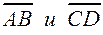
 . Следовательно, ABCD является параллелограммом и ромбом (поскольку длины всех сторон равны). Осталось доказать, что
. Следовательно, ABCD является параллелограммом и ромбом (поскольку длины всех сторон равны). Осталось доказать, что 



