Задачи для самостоятельного решения. 1. Векторы и образуют угол , Найти:
1. Векторы
2. Векторы ними углы, равные вычислить:
3. Доказать, что может иметь место знак равенства? 4. Какому условию должны удовлетворять векторы вектор 5. Даны векторы
6. Вычислить, какую работу производит сила 7. Вычислить, какую работу производит равнодействующая трех сил перемещении материальной точки из
8. Даны вершины четырехугольника A(1; –2; 2), B(1; 4; 0), С (–4; 1; 1) и D(–5; –5; 3). Доказать, что его диагонали AC и BD взаимно перпендикулярны. 9. Определить, при каком значении t векторы 10. Даны векторы 1)косинус угла между ними, 2) проекцию вектора 3) проекцию вектора 4) орт вектора 5) орт вектора 6) найти направляющие косинусы вектора 7) найти направляющие косинусы вектора 11. Даны вершины треугольника A(–1; –2; 4), B(–4; –2; 0) и С(3; –2; 1). Определить его внутренний угол при вершине B. 12. Даны вершины треугольника A (3; 2; –3), B(5; 1; –1) и С(1; –2; 1). Определить его внешний угол при вершине A. 13. Даны вершины треугольника A(1; 2; 1), В(3; –1; 7), С (7; 4; –2), убедиться, что этот треугольник равнобедренный. 14. Даны вершины четырехугольника A(11; 3; 3), B(12; –1; 3), С(4; –3; 2) и D(3; 1; 2). Доказать, что ABCD является прямоугольником, но не является квадратом. 15. Вектор образует острый угол с осью OZ. Зная, что его координаты. 16. Вектор
координаты, зная, что 17. Найти вектор
|

 и
и  образуют угол
образуют угол  ,
,  Найти:
Найти: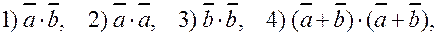

 .
.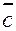 образует с
образует с . Зная, что
. Зная, что  ,
,
 .
.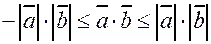 . В каких случаях здесь
. В каких случаях здесь был ортогонален к вектору
был ортогонален к вектору 
 и
и  . Вычислить:
. Вычислить:

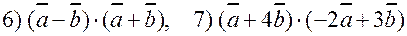 .
. при перемещении материальной точки из
при перемещении материальной точки из  в
в  .
. при
при в
в .
. и
и  взаимно перпендикулярны.
взаимно перпендикулярны. и
и 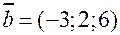 . Найти:
. Найти: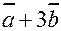 на вектор
на вектор  ;
; ;
; ,
, , найти
, найти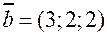 ,
, , образует с осью OY тупой угол. Найти его
, образует с осью OY тупой угол. Найти его .
. ,
,  и удовлетворяет условию
и удовлетворяет условию , где
, где  .
.


