Пусть  . Тогда
. Тогда

Пример 11. Векторы  и
и  образуют угол
образуют угол  ,
,  Найти длину вектора
Найти длину вектора  .
.
Решение. Пользуясь свойствами векторного произведения, раскрываем скобки и вычисляем каждое из слагаемых, пользуясь определением,  Осталось найти
Осталось найти 
Пример 12. Найти момент силы  , приложенной в точке
, приложенной в точке  , относительно точки
, относительно точки  ;
;
Решение. Искомый момент равен векторному произведению  Находим
Находим  , а затем и
, а затем и
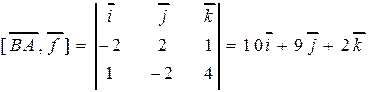
Пример 13. Даны векторы  и
и  . Найти вектор
. Найти вектор 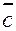 , который:
, который:
а) ортогонален  и
и  ;
;
б) образует с вектором  острый угол;
острый угол;
в) имеет длину равную 2.
Решение. Векторы  и
и  неколлинеарны, поскольку
неколлинеарны, поскольку  . Следовательно, все векторы им ортогональные, коллинеарны друг другу. В частности, вектор
. Следовательно, все векторы им ортогональные, коллинеарны друг другу. В частности, вектор 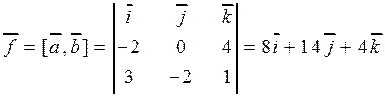 ортогонален
ортогонален  и
и  и отличен от
и отличен от  . Любой коллинеарный
. Любой коллинеарный  вектор может быть разложен по
вектор может быть разложен по  . То есть, вектор
. То есть, вектор 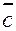 может быть представлен в виде
может быть представлен в виде  , где
, где  - неизвестное число. Осталось найти его:
- неизвестное число. Осталось найти его:
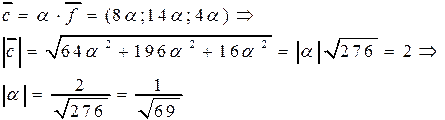
Знак  определим из того, что
определим из того, что 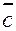 и
и  образуют острый угол, а это, значит, что
образуют острый угол, а это, значит, что 

Пример 14. Даны точки  Найти длину высоты треугольника
Найти длину высоты треугольника  , опущенной из вершины
, опущенной из вершины 
Решение. В примере 10 уже установлено, что треугольник  прямоугольный,
прямоугольный,  - катет и, следовательно, искомая высота равна
- катет и, следовательно, искомая высота равна 
Решим задачу иным способом. Пусть  – площадь треугольника
– площадь треугольника  , а
, а  – высота, опущенная на сторону
– высота, опущенная на сторону  .
.
Тогда  Заметим также, что площадь параллелограмма, построенного на векторах
Заметим также, что площадь параллелограмма, построенного на векторах  и
и  равна
равна
 , с одной стороны, и равна
, с одной стороны, и равна  , с другой.
, с другой.
Найдем векторы сторон. 
 .
.
 .
.
Вычислим длины векторов

Следовательно,


 . Тогда
. Тогда
 и
и  образуют угол
образуют угол  ,
,  Найти длину вектора
Найти длину вектора  .
. Осталось найти
Осталось найти 
 , приложенной в точке
, приложенной в точке  , относительно точки
, относительно точки  ;
; Находим
Находим  , а затем и
, а затем и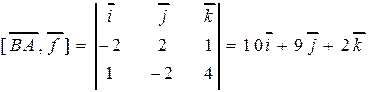
 и
и  . Найти вектор
. Найти вектор 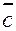 , который:
, который: острый угол;
острый угол; . Следовательно, все векторы им ортогональные, коллинеарны друг другу. В частности, вектор
. Следовательно, все векторы им ортогональные, коллинеарны друг другу. В частности, вектор 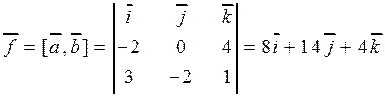 ортогонален
ортогонален  . Любой коллинеарный
. Любой коллинеарный  вектор может быть разложен по
вектор может быть разложен по  , где
, где  - неизвестное число. Осталось найти его:
- неизвестное число. Осталось найти его: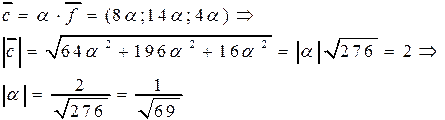
 образуют острый угол, а это, значит, что
образуют острый угол, а это, значит, что 

 Найти длину высоты треугольника
Найти длину высоты треугольника  , опущенной из вершины
, опущенной из вершины 
 - катет и, следовательно, искомая высота равна
- катет и, следовательно, искомая высота равна 
 – площадь треугольника
– площадь треугольника  – высота, опущенная на сторону
– высота, опущенная на сторону  .
. Заметим также, что площадь параллелограмма, построенного на векторах
Заметим также, что площадь параллелограмма, построенного на векторах  и
и  равна
равна , с одной стороны, и равна
, с одной стороны, и равна  , с другой.
, с другой.
 .
. .
.




