Линейные операции над векторами. Линейными операциями называются сложение векторов и умножение вектора на число.
Линейными операциями называются сложение векторов и умножение вектора на число. Определение 3. Пусть даны два вектора Сложением векторов называют операцию, сопоставляющую двум векторам их сумму.
 
Определение 4. Произведением вектора а) б) вектор в) векторы Умножение вектора на число — операция, сопоставляющая вектору и числу произведение вектора на это число. Свойства линейных операций 1) 2) ( 3) 4) Для любого вектора
Вектор Разностью двух векторов Базис Два (три) вектора называются упорядоченной парой (тройкой) векторов, если указано, какой из этих векторов является первым, какой – вторым, а какой – третьим (в случае трех векторов). Определение 5. Базисом в пространстве называется упорядоченная тройка некомпланарных векторов. Базисом на плоскости называется упорядоченная пара неколлинеарных векторов на этой плоскости. Базисом на прямой называется любой ненулевой вектор на этой прямой. Пусть называется линейной комбинацией векторов Если вектор Определение 6. Если Замечание. Все формулы в дальнейшем приводятся для базиса в пространстве. В случае базиса на плоскости, следует считать в формулах третью компоненту всех векторов равной нулю или полагать, что она, как и третий вектор базиса, отсутствует.
Теорема 1. Каждый вектор, параллельный какой-либо прямой, может быть разложен по базису на этой прямой. Каждый вектор, параллельный какой-либо плоскости, может быть разложен по базису на этой плоскости. Каждый вектор может быть разложен по базису в пространстве. Компоненты вектора в каждом случае определяются однозначно. Следствие. Равные векторы имеют одинаковые компоненты.
Теорема 2. При умножении вектора на число все его компоненты умножаются на это число. При сложении векторов их соответствующие компоненты складываются. Определение 7. Углом между ненулевыми векторами Таким образом, угол между векторами всегда лежит в диапазоне Определение 8. Базис называется ортонормированным, если все его векторы попарно ортогональны, а их длины равны 1.
Пример 1.
Из свойств квадрата и из определения операции умножения вектора на число получаем:
Осталось заметить, что:
Пример 2. 1)Выразить векторы 2) Построить векторы
Решение. 1)Из свойств параллелограмма и из определения операции суммы векторов получаем:
2) В процессе решения пункта 1) мы построили векторы
Пример 3. Решение. Пусть
По теореме косинусов
Складывая первое и третье равенства, находим:
Пример 4. Пусть Решение. Найдем координаты вектора
Требуется найти такие
Распишем это равенство в координатах:
Решаем систему методом Крамера:
Таким образом,
|

 и
и  . Построим равные им векторы
. Построим равные им векторы  и
и  (т. е, перенесем конец
(т. е, перенесем конец  называется суммой векторов
называется суммой векторов 
 называется вектор
называется вектор  ;
; ) Произведение вектора
) Произведение вектора  .
. =
=  , такой что
, такой что  ;
;


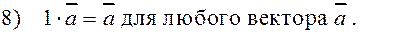
 называется противоположным к
называется противоположным к  и
и  .
. или коротко
или коротко  .
. векторы,
векторы,  произвольные числа. Выражение
произвольные числа. Выражение 
 .
.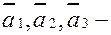 базис в пространстве и
базис в пространстве и  то числа
то числа  называются компонентами (или координатами) вектора
называются компонентами (или координатами) вектора  означает, что компоненты вектора
означает, что компоненты вектора 
 и
и  , где
, где  ,
,  .
. . Если угол между векторами равен
. Если угол между векторами равен  , то говорят, что эти векторы ортогональны.
, то говорят, что эти векторы ортогональны. квадрат, точки E,F,G,H лежат на сторонах AB, BC, CD, DA, соответственно, а О – точка пересечения диагоналей. Кроме того,
квадрат, точки E,F,G,H лежат на сторонах AB, BC, CD, DA, соответственно, а О – точка пересечения диагоналей. Кроме того,  Выразить векторы
Выразить векторы  через векторы
через векторы 
 Решение. Сразу заметим, что
Решение. Сразу заметим, что  неколлинеарны, а потому образуют на плоскости базис. Значит, любой вектор плоскости может быть разложен по
неколлинеарны, а потому образуют на плоскости базис. Значит, любой вектор плоскости может быть разложен по 





 через векторы
через векторы 
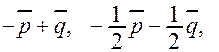






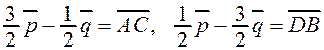


 Тогда
Тогда 







 . Разложите вектор
. Разложите вектор  по векторам
по векторам  , если это возможно.
, если это возможно.
 , что
, что  .
.
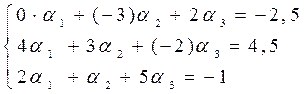






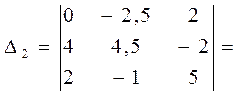





 и
и .
.


