Векторная алгебра. Задача 1. Найти координаты векторного произведения , если , .
Задача 1. Найти координаты векторного произведения Решение. Найдем Задача 2. Силы
Решение. Найдем силу сил
Задача 3. Даны вершины треугольника
Векторное произведение
Так как
Задача 4. Даны координаты вершин параллелепипеда: Решение. По определению, объем параллелепипеда равен смешанному произведению векторов, на которых он построен. Найдем эти векторы:
Объем этого параллелепипеда С другой стороны, объем параллелепипеда
Угол между вектором и гранью
так как вектор
Итак: Задача 5. Проверить, лежат ли в одной плоскости точки Решение. Найдем три вектора:
Три вектора лежат в одной плоскости, если они компланарны, т. е. их смешанное произведение равно нулю:
Решая эту систему, получим
ничным, если
Задача 7. Даны координаты вершин пирамиды 1. Найти длину вектора 2. Найти угол между векторами 3. Найти проекцию вектора 4. Найти площадь грани АВС. 5. Найти объем пирамиды ABCD. Координаты векторов: 1. Длина вектора
3. Проекция вектора
4.
5.
Векторная алгебра
В математике исследуются различные объекты. К числу основных относятся скалярные и векторные величины. Знакомство с ними состоялось еще в средней школе. Известно, что скалярная величина (скаляр) определяется одним параметром – величиной, например, 3, -5, 3.14 и так далее. В дальнейшем скаляры будем обозначать буквами Вектор – это направленный отрезок, характеризуемый двумя параметрами – длиной и направлением. Чтобы отличать векторы от скаляров, их будем задавать следующим образом Исторически сложилось, что геометрия оперирует со свободными векторами. Два вектора считаются равными, если одинаковы их длины и они сонаправлены (параллельны и направлены в одну сторону). Другими словами, действие вектора на объект не зависит от точки его приложения.
Итак, векторная алгебра строится для свободных векторов, что значительно упрощает теорию. При переходе к силам, действующим на тело, делаются определенные поправки (вводятся моменты сил), чем устраняется указанное противоречие. Введем понятие орта - единичного вектора, то есть вектора, длина которого равна единице. Обозначим длину, или модуль вектора Проекцией вектора
Рисунок 1. Векторы называются коллинеарными, если лежат на параллельных прямых. Векторы называются ортогональными, если угол между ними прямой. Векторы, лежащие в некоторой плоскости или параллельные плоскости, называются компланарными. Компланарные векторы могут быть перемещены в одну плоскость, сто следует из определения свободных векторов.
Линейными операциями над векторами называются сложение векторов, их вычитание, умножение на число (скаляр).
Правило параллелограмма.
Сложение двух векторов осуществляется следующим образом. В силу того, что векторы свободны, с помощью параллельного переноса совмещаются их начальные точки, затем на этих векторах, как на сторонах, строится параллелограмм. Диагональ параллелограмма, идущая из общей начальной точки является суммарным вектором этих дух векторов.
Рисунок 2.
Это правило установлено еще в древности путем наблюдений за передвижением предметов под действием двух сил.
Из правила параллелограмма можно получить правило треугольника суммирования двух векторов. Сумму векторов можно получить, построив вначале вектор
Сложение большего количества векторов осуществляется по правилу многоугольника. Заключается оно в следующем. Строится первый вектор, из его конца проводится второй вектор, из конца второго третий и так далее, затем соединяется начальная точка первого вектора с концом второго это и будет суммарным вектором. Правило доказывается с помощью несколько раз примененного правила треугольника.
Рисунок 3.
Правило вычитания векторов
Разностью векторов
Рисунок 4. Представим вектор
Правило умножения вектора на число
Вектор
Примечание. Приведенные выше правила требуют решения соответствующих задач построением, то есть с помощью чертежей, что не всегда удобно ввиду неизбежных погрешностей построения. Встает вопрос, как свести эти ошибки к минимуму. Одним из решений этого вопроса явилось введение базисов, о чем пойдет речь ниже.
Базисы на плоскости и в трехмерном пространстве
Определение 1. Любые два неколлинеарных вектора могут быть выбраны в качестве базиса на плоскости. Определение 2. Любые три некомпланарных вектора могут быть выбраны в качестве базиса в трехмерном пространстве. Определение 3. Базис называется ортогональным, если углы между базисными векторами прямые. Определение 4. Базис называется нормированным, если базисные векторы единичные. Определение 5. Базис называется ортонормированным, если он ортогональный и нормированный. Векторы ортонормированного базиса в соответствии с существующими традициями обозначаются Определение 6. Линейной комбинацией векторов
Теорема 1. Любой вектор Доказательство. Совместим начальные точки базисных векторов и вектора
Поскольку векторы
Рисунок 5.
Очевидно, векторы
Теорема 2. Любой вектор трехмерного пространства может быть представлен в виде линейной комбинации базисных векторов. Докажем теорему для ортонормированного базиса, то есть, что
Пусть точка
Рисунок 6.
Следствие. Векторы считаются равными, если равны их соответствующие координаты в одном и том же базисе. То есть
Вместо обозначения Имеют место две теоремы о проекциях векторов: 1. 2. Из этих теорем следуют правила сложения, вычитания векторов, заданных в базисе, умножения вектора на скаляр. Итак, Пусть
Аналогично
или
Скалярное произведение векторов
Определение. Скалярным произведением двух векторов
Знак скалярного произведения определяется знаком косинуса. Очевидно, скалярное произведение можно представить в виде
Как уже говорилось ранее, правило суммирования векторов было получено еще в древности из наблюдений за движением тел под действием нескольких сил. Правило вычитания векторов следовало из правила их суммирования. Правило умножения вектора на число также следовало из наблюдений за действием на тело сил. Скалярное произведение также следует из практических потребностей. В самом деле, если тело под действием силы
то есть совершаемая работа вычисляется посредством скалярного произведения. Если угол
Свойства скалярного произведения
1. 2.
Доказательство для случая 3. Доказательство. 4. 5.
Скалярное произведение векторов в ортонормированном базисе
Пусть Доказательство.
Данный результат следует из 3 – го свойства скалярного произведения. Поскольку базис
Приложения скалярного произведения
1. Условие ортогональности векторов: из 2. Длина вектора 3. Угол между векторами. Из определения скалярного произведения
4. Расстояние между точками. Для получения этого результата введем декартову систему координат, которая известна еще со школы. Осью координат (координатной осью) называют прямую, на которой выбрана начальная точка (начало отсчета), положительное направление и единица масштаба. Совместим начальные точки векторов ортонормированного базиса Введение системы координат дает возможность применить, так называемый, координатный метод, увязывающий точку, как геометрический объект, с тройкой чисел, называемых координатами точки. Тройка называется упорядоченной, поскольку взаиморасположение чисел зафиксировано. Первое число - есть координата вдоль оси Любой объект теперь можно считать множеством точек. Введем понятие радиуса-вектора точки Пусть даны две точки
Таким образом, длина вектора
Пример. 1. Задан треугольник с вершинами
Длину стороны определяем как расстояние между вершинами, тогда
Определим векторы
Угол между этими векторами есть угол при вершине
Угол теперь определяется с помощью таблиц или калькулятора
Векторное произведение
Как уже говорилось выше, скалярное произведение векторов имеет практическое значение. В частности, с его помощью определяется работа силы на участке пути. Векторное произведение также имеет практический смысл. С его помощью определяют моменты сил, придающие телам вращение.
Правая и левая тройки векторов
Определение 1. Тройка некомпланарных векторов называется правой, если с конца третьего вектора кратчайший поворот от первого вектора ко второму виден против часовой стрелки. Определение 2. Тройка некомпланарных векторов называется левой, если с конца третьего вектора кратчайший поворот от первого вектора ко второму видится по часовой стрелке.
Можно проверить, что правая тройка векторов связана на практике с правой резьбой, левая тройка – с левой резьбой.
Это обстоятельство привело к тому, что до середины XX века наука о движении (механика) излагалась как в правой, так и в левой декартовых системах координат, что затрудняло изучение литературы по предмету. В середине XX века договорились использовать только правую тройку векторов, а, следовательно, правую декартову систему координат. На рисунке 7 тройка базисных векторов
Рисунок 7.
Определение векторного произведения, его свойства. Векторным произведением двух векторов называется третий вектор, длина которого равна произведению модулей перемножаемых векторов на синус угла между ними, направлен этот вектор перпендикулярно плоскости, в которой расположены перемножаемые векторы, образуя с ними правую тройку. Обозначения векторного произведения
Свойства векторного произведения 1. 2. 3.
4.
Векторное произведение векторов в ортонормированном базисе
Если
Доказательство. Рассмотрим векторные произведения базисных векторов.
Вычислим
Этот результат следует из 3 – го свойства скалярного произведения. Очевидно первое, пятое и девятое слагаемые в правой части формулы равны нулю как произведения коллинеарных векторов. Далее
Итак,
что и требовалось доказать.
Замечание 1. Определитель третьего порядка в этой формуле называют иногда символическим, поскольку не все свойства обычных определителей для него справедливы. Это связано с тем, что одна из строк состоит из векторов, элементы двух других - скаляры. Его использование оправдано тем, что после записания векторного произведения его легко представить в обычном виде, разложив определитель по элементам, скажем, первой строки. Замечание 2. Условием коллинеарности векторов является равенство нулю их векторного произведения. Следовательно, символический определитель должен быть равен нулю, для этого достаточно, чтобы любые две его строки, или два столбца были пропорциональны. Столбцы пропорциональными быть не могут, так как базисные векторы не коллинеарны, а значит не пропорциональны, строка из векторов не может быть пропорциональна строке из скаляров по той же причине. Остается пропорциональность двух последних строк определителя. Итак, условием коллинеарности векторов
Пример. Определить площадь треугольника, заданного вершинами Поскольку площадь параллелограмма, построенного на векторах Вычислим
Смешанное произведение трех векторов
Смешанным произведением трех векторов Модуль смешанного произведения Для векторов смешанное произведение
Доказательство. Так как
Правая часть последней формулы является разложением приведенного выше определителя по элементам третьей строки, что доказывает формулу.
Пример. Вычислить объем параллелепипеда, заданного векторами Вычислим Объем этого параллелепипеда равен 10.
Примеры для самоподготовки.
6.1. Вычислить вектор
6.2. Определить скалярное произведение векторов 6.3 Определить скалярное произведение векторов 6.4. Определить длину векторного произведения векторов
6.5. Определить длину векторного произведения 6.6 Установить, при каком значении 6.7. Проверить коллинеарность векторов 6.8. Проверить при каком
|

 , если
, если  ,
,  .
. и
и  . Векторное произведение, по определению, равно
. Векторное произведение, по определению, равно 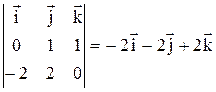 .
. и
и 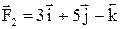 приложены к точке
приложены к точке 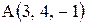 . Вычислить величину момента равнодействующей этих сил
. Вычислить величину момента равнодействующей этих сил  относительно точки
относительно точки  .
. :
:  . Момент
. Момент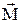 вычисляется по формуле
вычисляется по формуле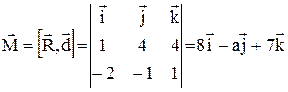 , а его модуль
, а его модуль  .
. Найти его площадь и длину высоты, опущенной из вершины С.
Найти его площадь и длину высоты, опущенной из вершины С. . Находим векторы
. Находим векторы 








 где
где  длина высоты, опущенной из вершины С на сторону АВ,
длина высоты, опущенной из вершины С на сторону АВ,  .
. 


 . Найти объем параллелепипеда, его высоту, опущенную из вершины С, угол между вектором AD и гранью, в которой лежат векторы АВ и АС.
. Найти объем параллелепипеда, его высоту, опущенную из вершины С, угол между вектором AD и гранью, в которой лежат векторы АВ и АС. .
. .
.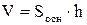 ,
,  - это площадь параллелограмма:
- это площадь параллелограмма:  .
. , тогда высота
, тогда высота 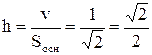 .
. найдем по формуле
найдем по формуле .
. перпендикулярен грани, в которой лежат векторы
перпендикулярен грани, в которой лежат векторы 
 . Угол между этим вектором и вектором
. Угол между этим вектором и вектором  находим по известной формуле
находим по известной формуле . Очевидно, что искомый угол
. Очевидно, что искомый угол 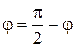 .
. .
. ,
,  . Найти линейную зависимость вектора
. Найти линейную зависимость вектора  , если это возможно.
, если это возможно. .
. .
. . Следовательно, эти три вектора линей-
. Следовательно, эти три вектора линей- но зависимы. Найдем линейную зависимость
но зависимы. Найдем линейную зависимость  от
от  .
.
 .
. , т.е.
, т.е.  .
. Задача 6. При каком ненулевом значении t вектор
Задача 6. При каком ненулевом значении t вектор  будет еди-
будет еди-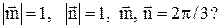 Вектор будет единичным, если его длина будет равна единице, т. е.
Вектор будет единичным, если его длина будет равна единице, т. е.  .
.




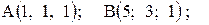
 ;
; 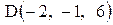 .
. .
. .
.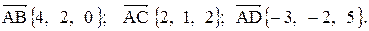

 2.
2. 

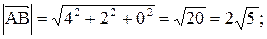





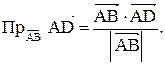
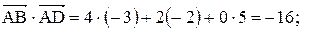







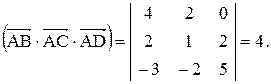


 и так далее.
и так далее. , в последнем случае
, в последнем случае  начальная,
начальная,  конечная точки вектора. Иногда их обозначают жирным шрифтом a.
конечная точки вектора. Иногда их обозначают жирным шрифтом a.
 , тогда единичный вектор
, тогда единичный вектор  .
. на направление
на направление  , где
, где 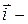 единичный вектор, показывающий направление от
единичный вектор, показывающий направление от  к
к  , является скалярная величина
, является скалярная величина  . В соответствии с рисунком
. В соответствии с рисунком  , следовательно, если угол между векторами
, следовательно, если угол между векторами  , в противном случае проекция отрицательна.
, в противном случае проекция отрицательна.

 , затем из его конца провести вектор
, затем из его конца провести вектор 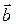 . Вектор, идущий из начала первого вектора в конец второго является суммой этих двух векторов, что непосредственно следует из рисунка 2.
. Вектор, идущий из начала первого вектора в конец второго является суммой этих двух векторов, что непосредственно следует из рисунка 2.
 является вторая диагональ параллелограмма, проведенная из конца вычитаемого вектора в конец уменьшаемого. Это правило доказывается с помощью рисунка 4.
является вторая диагональ параллелограмма, проведенная из конца вычитаемого вектора в конец уменьшаемого. Это правило доказывается с помощью рисунка 4.
 . Очевидно,
. Очевидно,  , но эта сумма 0 - есть диагональ нижнего параллелограмма. Из среднего параллелограмма видно, полученный вектор совпадает с вектором, являющимся второй диагональю исходного (верхнего) параллелограмма, что требовалось доказать.
, но эта сумма 0 - есть диагональ нижнего параллелограмма. Из среднего параллелограмма видно, полученный вектор совпадает с вектором, являющимся второй диагональю исходного (верхнего) параллелограмма, что требовалось доказать.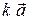 , где
, где  скаляр, представляет собой вектор, длина которого в
скаляр, представляет собой вектор, длина которого в  раз больше длины вектора
раз больше длины вектора  и в противоположном направлении при
и в противоположном направлении при  отрицательном.
отрицательном. .
. называется выражение
называется выражение  , где
, где  некоторые числа (скаляры).
некоторые числа (скаляры). :
:  .
. , из конца вектора
, из конца вектора  ) проведем прямые, параллельные векторам
) проведем прямые, параллельные векторам  и
и  (рисунок 5). Из правила сложения векторов следует
(рисунок 5). Из правила сложения векторов следует .
. и
и  коллинеарны, можно записать
коллинеарны, можно записать  , где
, где  . Аналогично
. Аналогично  , где
, где  , причем
, причем  и
и  могут быть как положительными, так и отрицательными числами в зависимости от направлений базисных векторов и вектора
могут быть как положительными, так и отрицательными числами в зависимости от направлений базисных векторов и вектора 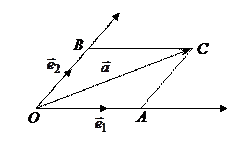
 .
. начальная точка векторов
начальная точка векторов  ,
,  конечная точка вектора
конечная точка вектора  основание перпендикуляра, опущенного из точки
основание перпендикуляра, опущенного из точки  на плоскость
на плоскость  . Из треугольника
. Из треугольника  , изображенного на рисунке 6, следует
, изображенного на рисунке 6, следует  . Из первой теоремы следует
. Из первой теоремы следует  , из коллинеарности векторов
, из коллинеарности векторов  и
и  следует
следует  , очевидно,
, очевидно, 
 , если
, если  .
. , если базисные векторы заданы ранее.
, если базисные векторы заданы ранее. ,
, где
где  число (скаляр).
число (скаляр). ,
,  , тогда
, тогда , или
, или 
 Таким образом, чтобы просуммировать два, или большее количество векторов, заданных в едином базисе, необходимо просуммировать их одноименные проекции.
Таким образом, чтобы просуммировать два, или большее количество векторов, заданных в едином базисе, необходимо просуммировать их одноименные проекции. ,
, (
( .
. называется число, равное произведению модулей этих векторов на косинус угла между ними.
называется число, равное произведению модулей этих векторов на косинус угла между ними. .
. .
. ,
, острый, работа положительная (активная). При тупом угле между векторами, работа отрицательная, то есть совершается силами, противодействующими движению (например, силой трения).
острый, работа положительная (активная). При тупом угле между векторами, работа отрицательная, то есть совершается силами, противодействующими движению (например, силой трения). . Поскольку
. Поскольку 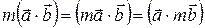 , если
, если 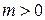 это свойство очевидно: поскольку
это свойство очевидно: поскольку  в этом случае сонаправлены,
в этом случае сонаправлены, .
. не приводится.
не приводится. .
. .
.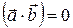 , когда
, когда  . Если исключить из рассмотрения нуль-векторы, то скалярное произведение равно нулю при
. Если исключить из рассмотрения нуль-векторы, то скалярное произведение равно нулю при  , то есть при
, то есть при 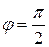 .
. , то есть квадрат длины вектора равен скалярному произведению вектора на себя.
, то есть квадрат длины вектора равен скалярному произведению вектора на себя. , то есть скалярное произведение векторов в этом случае – есть сумма произведений одноименных проекций перемножаемых векторов.
, то есть скалярное произведение векторов в этом случае – есть сумма произведений одноименных проекций перемножаемых векторов.
 - ортонормированный, векторы, входящие во второе, третье, четвертое, шестое, седьмое и восьмое скалярные произведения, ортогональны, следовательно, эти произведения равны нулю (четвертое свойство). Кроме того, из второго и пятого свойств имеем
- ортонормированный, векторы, входящие во второе, третье, четвертое, шестое, седьмое и восьмое скалярные произведения, ортогональны, следовательно, эти произведения равны нулю (четвертое свойство). Кроме того, из второго и пятого свойств имеем  ,
,  ,
, 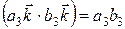 . Теорема доказана.
. Теорема доказана. .
. .
. следует
следует .
.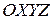 . Базисный вектор
. Базисный вектор 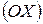 , вектор
, вектор  - по оси ординат
- по оси ординат  , вектор
, вектор  .
. , второе – вдоль
, второе – вдоль 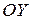 , третье – расстоянии вдоль оси
, третье – расстоянии вдоль оси  . Меняя местами любые из этих чисел, получаем другую точку пространства. Например,
. Меняя местами любые из этих чисел, получаем другую точку пространства. Например,  и
и  - разные точки пространства. Начало координат соответствует тройке
- разные точки пространства. Начало координат соответствует тройке  .
. – это вектор, начальной точкой которого является начало координат, конечной – точка
– это вектор, начальной точкой которого является начало координат, конечной – точка  , нетрудно заметить, что радиус-вектор точки может быть представлен в виде
, нетрудно заметить, что радиус-вектор точки может быть представлен в виде  .
. и
и  . Вместе с вектором
. Вместе с вектором  радиусы-векторы точек
радиусы-векторы точек  и
и  представляют треугольник
представляют треугольник  , причем
, причем .
. .
. . Определить длину стороны
. Определить длину стороны  и угол при вершине
и угол при вершине  .
. ,
, .
. .
. рад.
рад. левая.
левая.
 или
или  .
. . Доказательство этого свойства следует из того, что если поворот от
. Доказательство этого свойства следует из того, что если поворот от  по сравнению с
по сравнению с  , где
, где  .
. , если
, если  , но
, но  .
. ,
,  , векторное произведение векторов вычисляется с помощью формулы
, векторное произведение векторов вычисляется с помощью формулы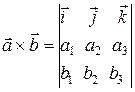 .
. как произведения коллинеарных векторов,
как произведения коллинеарных векторов,  , в самом деле,
, в самом деле, 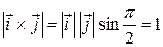 , то есть равен длине вектора
, то есть равен длине вектора  . Аналогично
. Аналогично  . Действительно длина векторного произведения
. Действительно длина векторного произведения  равна единице, как и длина вектора
равна единице, как и длина вектора  . Так же доказывается, что
. Так же доказывается, что  .
.
 ,
, ,
, .
. ,
, .
. ,
,  .
. , равна
, равна  , то есть длине векторного произведения этих векторов, площадь заданного треугольника равна половине площади параллелограмма, то
, то есть длине векторного произведения этих векторов, площадь заданного треугольника равна половине площади параллелограмма, то  .
. .
. В итоге
В итоге 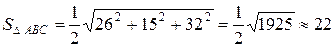 .
. называется число, равное векторному произведению
называется число, равное векторному произведению  , то есть
, то есть  .
. компланарны, то смешанное произведение
компланарны, то смешанное произведение 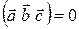 , что следует из определений векторного, скалярного и смешанного произведений.
, что следует из определений векторного, скалярного и смешанного произведений. ,
,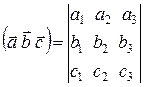 .
. ,
, .
. ,
,  ,
,  .
. ,
, , если
, если  .
. , угол между ними
, угол между ними  ?
?  .
. ,
,  .
.  .
. и
и .
.  .
. , если
, если  , угол между ними
, угол между ними  .
.  .
. векторы
векторы  ,
, 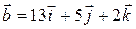 ортогональны?
ортогональны?  .
.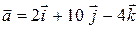 ,
,  .
. ,
, 


