Параметризация привязок

Из списка Ограничения видно, что на диагональ наложено три связи (рис. 330): две связи Совпадение точек обеспечивают принадлежность конечных точек отрезка углам прямоугольника, а связь Точка на середине кривой обеспечивает положение вспомогательной точки.

· Попробуйте перемещать отрезки за их управляющие узелки, и вы увидите, как система, выполняя наложенные на объекты параметрические зависимости, не позволяет их нарушить!

При построении параметрического изображения проверяйте его подобным образом, перемещая входящие в него объекты или их узелки, просматривая наложенные на объекты связи и ограничения.

Если изображение реагирует на такие перемещения так, как вы и ожидаете - можно продолжать построения. Если же нет - то необходимо немедленно остановиться, выяснить причину, устранить ее и только потом двигаться дальше. В противном случае трудоемкость исправления ошибки будет многократно возрастать.

Проставьте размеры высоты и ширины созданного прямоугольника.

Обратите внимание на то, что размерные надписи проставленных размеров заключены в рамку. Это признак ассоциированных фиксированных размеров. Они формируются при включенной опции Фиксировать размеры в диалоговом окне настройки параметризации.

Такие размеры остаются постоянными при любых изменениях изображения. В данном случае после их простановки вы уже не сможете изменять размеры прямоугольника перемещением его отрезков или узелков управления.

Теперь изменять геометрию изображения можно только изменением значений самих фиксированных размеров.

Просмотрите связи и ограничения вертикального размера. Для этого вызовите команду Показать/удалить ограничения (рис. 331).

Первая связь Совпадение точек обеспечивает связь размера с тремя отрезками в правом нижнем углу прямоугольника, вторая – с двумя отрезками и горизонтальным размером в правом верхнем углу прямоугольника, ограничение Фиксированный размер определяет его фиксированный статус.

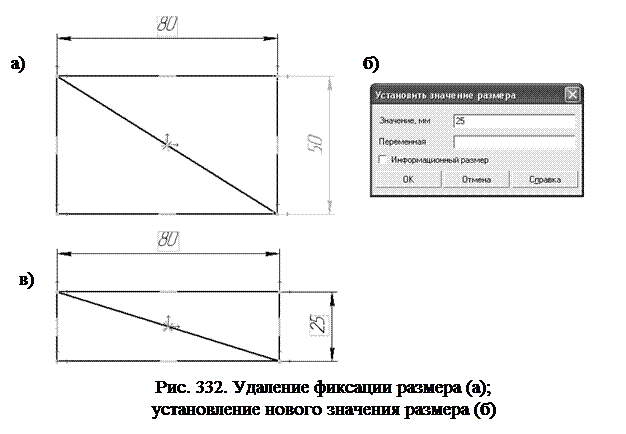
Кроме просмотра связей и ограничений список Показать/удалить ограничения обладает еще одной важной функцией. С помощью кнопки Удалить в виде крестика в верхней его части можно снять с объекта текущую (выделенную в списке цветом) связь или ограничение.

Например, выделите в списке ограничение Фиксированный размер (для размера 50), нажмите кнопку Удалить, закройте список щелчком на кнопке Ограничения и закончите работу нажатием кнопки Прервать команду на панели Специального управления панели Свойств.

Вертикальный размер 50 утратит свой фиксированный статус – теперь это свободный ассоциированный размер. Такие размеры не запрещают изменение изображения, а просто меняют свое значение в ходе редактирования геометрии (рис. 332 а, в).

· Измените высоту прямоугольника, изменив значение вертикального размера.

· Для этого дважды щелкните по размеру, он выделится цветом и появится диалоговое окно Установить значение размера (рис. 332б).Снимите галочку в поле Информационный размер и задайте в окне Значение величину 25. Щелчком по кнопке ОК закройте окно. После этого размер вновь станет фиксированным (рис. 332в).

Чтобы удалить все ограничения с одного или нескольких объектов, выполните следующее:

· любым способом выделите объекты, ограничения которых требуется удалить;

· нажмите кнопку Удалить все ограничения на расширенной инструментальной панели Показать/удалить ограничения панелиПараметризация.

Все ограничения выделенных объектов будут сняты. Вместе с ограничениями геометрических объектов удаляются ограничения всех ассоциированных с ними объектов оформления.