
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Провідники в електричному полі
Дата добавления: 2014-12-06; просмотров: 681
|
|
Вихідні дані Таблиці 8.2
| № вар | Позика (тис.грн.) | Термін погашення боргу (років) | Вартість кредиту (%) |
| 18,5 | |||
| 21,0 | |||
| 16,5 | |||
| 20,6 | |||
| 20,5 | |||
| 18,0 | |||
| 15,5 | |||
| 18,5 | |||
| 16,0 | |||
| 22,5 | |||
| 12,5 | |||
| 17,0 | |||
| 24,5 | |||
| 21,5 | |||
| 16,0 | |||
| 17,0 | |||
| 23,0 | |||
| 15,0 | |||
| 17,5 | |||
| 18,0 |
Розрахувати суму процентів і основного боргу. Дані занести в таблицю та накреслити графік.
Лабораторная работа № 10
Шифрование, дешифрование информации с применением криптографических алгоритмов перестановок
Цель работы
Криптоанализ и программная реализация алгоритмов перестановок для шифрования и дешифрования исходного текста.
Краткие теоретические сведения
Шифры перестановки
Шифр, преобразования из которого изменяют только порядок следования символов исходного текста, но не изменяют их самих, называется шифром перестановки (ШП).
Пусть имеем сообщение из n символов. Его можно представить с помощью таблицы:
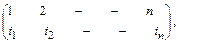
где i1 - номер места зашифрованного текста, на которое попадает I-ая буква исходного сообщения при выбранном преобразовании, i2 - номер места для II-й буквы и т.д. В верхней строке таблицы выписаны по порядку числа от 1 до n, а в нижней - те же числа, но в произвольном порядке. Такая таблица называется подстановкой степени n.
Зная подстановку, задающую преобразование, можно как зашифровать, так и расшифровать текст.
Например, если для преобразования используется подстановка:
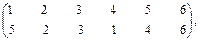
и в соответствии с ней зашифровывается слово МОСКВА, то получится слово КОСМВА.
Итак, используя метод математической индукции, определим, что существует n! вариантов заполнения нижней строки таблицы. Т.е. число различных преобразований шифра перестановки, предназначенного для зашифрования сообщения длины n, меньше либо равно n!. При больших n для вычисления n! можно пользоваться формулой Стирлинга:
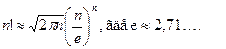 .
.
Примером ШП, предназначенного для зашифрования сообщения длины n, является шифр, в котором в качестве множества ключей взято множество всех подстановок степени n. Число ключей такого шифра =n!.
Для использования на практике такой шифр не удобен, т.к. при больших значениях n приходится работать с длинными таблицами.
| <== предыдущая лекция | | | следующая лекция ==> |
| Провідники, діелектрики, напівпровідники | | | Поляризація діелектрика |