Задание автоматов
Автоматы могут быть заданы следующими способами: 1. В виде графа
Рис. 1. Автомат Мили
Рис.2. Автомат Мура. При построении автомата Мили каждая дуга, соединяющая вершины Так как в автомате Мура выходной сигнал 2. В виде таблиц перехода и выхода (автомат Мили); отмеченной таблицы перехода (автомат Мура). Автомат Мили описывается с помощью двух таблиц: таблицы перехода и таблицы выхода:
Таблица переходов (ТП) Таблица выходов (ТВ)
Автомат Мура описывается с помощью отмеченной таблицы перехода: Таблица переходов (ТП)
Пример. Синтезировать автомат, на вход которого подаются монеты номинальной стоимостью 1, 2 и 3 копейки, а на выходе автомат выдает билет, если сумма набранных монет составляет 3 копейки, если сумма меньше 3 копеек, то автомат ничего не выдает, если сумма больше 3 копеек, то автомат возвращает деньги. Определим входной, выходной алфавиты и множество внутренних состояний: · входной алфавит · выходной алфавит · множество внутренних состояний где
Рис.3. Автомат Мили Таблицы перехода и выхода представлены в виде: Таблица переходов (ТП) Таблица выходов (ТВ)
Неопределенным состоянием называется несуществующее состояние. Частичным автоматом называется автомат, в котором некоторые состояния в таблице перехода не определены. Для дальнейшего исследования неопределенное состояние некоторым образом доопределяют.
|




 и
и 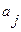 , имеет обозначение
, имеет обозначение  . Это означает следующее: находясь, в состоянии
. Это означает следующее: находясь, в состоянии  автомат, отрабатывая входной сигнал
автомат, отрабатывая входной сигнал  , выдает выходной сигнал
, выдает выходной сигнал  и переходит в состояние
и переходит в состояние  .
. зависит только от текущего состояния
зависит только от текущего состояния 







 - монеты номинальной стоимостью 1, 2 и 3 копейки
- монеты номинальной стоимостью 1, 2 и 3 копейки - на выходе возможны выходные символы:
- на выходе возможны выходные символы:  - ничего;
- ничего;  - билет;
- билет;  - возврат.
- возврат. ,
, - «в автомате 3 копейки».
- «в автомате 3 копейки». Граф автомата имеет вид:
Граф автомата имеет вид:


