Задача о числе подмножеств данного множестваПусть имеется М={ 0-если соответствующий элемент не входит в подмножество. 1-если входит. Например, подмножеству { Для вех подмножеств получим (0, 0, 0, …0), (1, 0, 0, …0), (0, 1, 0, 0,..., 0)… (1, 1, 1, …1) Кортежей столько, сколько подмножеств. Это размещения, состоящие из двух элементов (0 и 1) и отличающиеся друг от друга либо элементами, либо их порядком. Это размещения с повторениями из двух по n: Получим Ậ Таким образом, мы доказали теорему: Число подмножеств n-элементного множества равно Следствие: Так как число пустых подмножеств С
|
, 
}. Пустое множество Ø входит в это множество как подмножество. Одноэлементные множества тоже. Поставим каждому подмножеству кортеж длиной n, состоящий из 0 и 1.
} будет соответствовать кортеж 010100000….0000…
= 
.
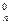(0)=1, одноэлементных-С 
= n, двухэлементных-С 
, трехэлементных-С 
, n-элементных С 
, то сумма 
С 
= 
