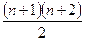Лекция 16. Метод математической индукции
Метод математической индукции - не просто распространенный метод решения олимпиадных задач, но и способ доказательства многих утверждений в математической науке. (Не случайно эта лекция такая длинная!) Поэтому знать этот метод нужно не только математику-олимпиаднику, но и каждому, кто собирается в дальнейшем изучать высшую математику или теорию алгоритмов. Что же такое индукция? Часто индукцию сравнивают с падением ряда доминошек: мы толкаем первую доминошку - она падает и задевает вторую. Вторая доминошка от этого тоже падает и задевает третью. Теперь падает третья доминошка, задевает четвертую... - и в итоге падает весь ряд. А происходит это по двум причинам: 2.) Любая доминошка, падая, задевает следующую. Доказательство по индукции протекает аналогичным образом. У нас есть ряд утверждений (обычно - бесконечно длинный), которые надо доказать. И для этого достаточно доказать всего два утверждения: 1.) База индукции: первое утверждение ряда верно. 2.) Переход индукции: если верно какое-то утверждение ряда (неважно, какое именно ), то верно и следующее за ним утверждение ряда. (эти два пункта аналогичны пунктам про падающие доминошки!) Почему же тогда верны все утверждения ряда? Первое утверждение верно по базе индукции. По переходу индукции мы получаем, что если верно первое утверждение ряда, то верно и второе. Значит, верно и второе утверждение. Еще раз применяем переход: если верно второе утверждение, то верно и третье. Значит, третье утверждение тоже верно. Сделав еще один такой шаг, мы получим, что вернои четвертое утверждение. Затем - пятое, шестое... десятое... сотое... тысячное... миллионное... В общем, верно утверждение ряда со сколь угодно большим номером, то есть любое, то есть каждое - что и требовалось доказать. Пример. Из квадрата 16x16 клеток вырезали одну клетку. Докажите, что полученную фигуру можно разрезать на уголки из трех клеток.
Теперь перейдем от 4x4 к 8x8: квадратик 8x8 составен из четырех квадратиков 4x4. В одном из них есть вырезанная клетка, а в остальных трех мы вырежем по клетке, отрезав прилежащий к центру уголок (аналогично предыдущему). Теперь образуется 4 квадратика 4x4, в каждом из которых вырезана клетка. Каждый из них мы умеем разрезать на уголки - значит, разрежем и весь квадрат 8x8. А от квадрата 8x8 можно точно так же перейти к квадрату 16x16, составив его из четырех частей - получаем ч.т.д (пример разрезания всего квадрата 16x16 на уголки - см. рис. внизу).
Решение №2. (то же самое, но с волшебным словом " индукция") Докажем по индукции следующее утверждение: квадрат 2nx2n с одной вырезанной клеткой можно разрезать на уголки из трех клеток.(На самом деле, здесь спрятан бесконечный ряд утверждений: про квадрат 2x2, 4x4, 8x8, 16x16... 1024x1024 и т.д.) Замечание: предположением индукции называется предположение о верности очередного утверждения ряда, из верности которого мы в переходе индукции доказываем верность следующего утверждения ряда. (!) Когда задача решается по индукции, то решение записывается в стиле, похожем на решение №2. Но придумывается оно часто в стиле решения №1 - так бывает удобнее, особенно для начинающих; -) Пример. Докажите, что число из 243 единиц делится на 243. Решение №2: (опять то же самое, но сторого индуктивно записанное) Докажем по индукции утверждение: число из 3n единиц делится на 3n (т.е. бесконечный ряд утверждений при разных натуральных n). База: 111 делится на 3 (n=1). Святая правда. В частном 37 получается. Мы заметили некоторую закономерность в значениях изучаемой последовательности. Проверяем эту закономерность для n=1. Предполагаем, что формула справедлива при некотором n и доказываем, что она справедлива для n=n+1. Подставляем в формулу n+1 и получаем формулу, которой соответствует (n+1) – ый член. Затем получаем (n+1) – ый член, исходя из общего принципа построения последовательности. Получим формулу для n+1. Если эти формулы совпадают, то закономерность считается доказанной. Пример: S Получим эту формулу из общих соображений. Sn+1 = Sn + n +1 = Что и требовалось доказать. Пример. Докажите, что 1+2+...+N=N(N+1)/2 (такие числа называются " треугольными": 1, 3, 6, 10, 15, 21, 28...). Решение: Докажем по индукции (обычно говорят " докажем индукцией по N", т.е. по переменной, значением которой нумеруются утверждения в ряду). Переход: Пусть тождество верно для какого-то значения N, которое мы теперь тоже обозначим за N. Надо доказать, что оно верно и для значения, на 1 большего, т.е. (в новом смысле буквы N) для N+1. Теперь предположение индукции будет выглядеть, как 1+2+...+N=N(N+1)/2, а то, что надо доказать - как результат подстановки сюда N+1 вместо N, т.е. 1+2+...+N+(N+1)=(N+1)(N+2)/2. Техническая часть - из одного равенства вывести другое - трудностей не представляет: 1+2+...+N+(N+1) = N(N+1)/2+(N+1) - по предположению индукции (т.е. по первому равенству). А это равно (N+1)(N/2+1) = (N+1)(N+2)/2, ч.т.д. Пример. Докажите, что 1+3+...+(2N-1)=N2 - сумма первых N нечетных чисел равна N2. Переход: Предположение индукции: 1+3+...+(2N-1)=N2 - так и пишут в индуктивных доказательствах, скрывая ту подтасовку, которая была продемонстрирована в решении предыдущей задаче (и сбивая с толку тех, кто плохо понимает метод индукции!). Утверждение, которое надо доказать: 1+3+...+(2N-1)+(2*(N+1)-1) = (N+1)2 - т.е. 1+3+...+(2N-1)+(2N+1) = (N+1)2. Его левая часть, по предположению индукции - это N2+2N+1, что, конечно же, равно (N+1)2, ч.т.д. Пример. Докажите, что 2N> N при любом натуральном N. База: N=1 - действительно, 21=2> 1. Переход: Предположим, что при некотором N 2N> N. Теперь докажем, что 2N+1> N+1. Действительно, 2N+1=2*2N> 2N по предположению. А 2N> =N+1 при всех N (очевидно), откуда 2N+1> N+1, ч.т.д. Доказательство делимости по индукции мы уже видели в задаче 2. Вот еще один типичный пример: Пример. Докажите, что 32N+2+8N-9 делится на 16 при любом натуральном N. База: N=1 - действительно, 32*1+2+8*1-9=80 - делится на 16. Переход: Уже известная махинация сводит доказательство перехода к следующему утверждению: если 32N+2+8N-9 делится на 16, то 32(N+1)+2+8(N+1)-9 делится на 16. Последнее число равно 32N+4+8N+8-9 = 9*32N+2+8N+8-9 = 8*32N+2+32N+2+8N+8-9 = 8*(32N+2+1)+32N+2+8N-9 Сумма последних трех слагаемых делится на 16 по предположению, а первое - как произведение 8 и четного числа 32N+2+1, ч.т.д.
|



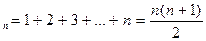 , при n=1 эта формула справедлива: Пусть она справедлива при некотором n. Если она справедлива для n+1, то должно быть S
, при n=1 эта формула справедлива: Пусть она справедлива при некотором n. Если она справедлива для n+1, то должно быть S 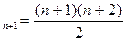 .
.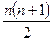 + n+1 = (n+1) (
+ n+1 = (n+1) (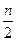 +1) =
+1) =