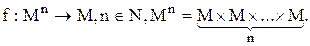Операции. Операциянад (на) множеством M это функция [7]:
Операция над (на) множеством M это функция [7]:
Из определения операции видно, что она замкнута на множестве М, т.е. результат операции не выходит за пределы этого множества. Еще одно свойство операции – однозначность результата, т.е. упорядоченный набор n элементов (операндов) дает в результате операции только один элемент. Порядок операции – это количество ее операндов: n = 1 соответствует унарной (монадической) операции, n = 2 – бинарной (диаедической) операции и т.д. Далее рассматриваются только бинарные операции. Они могут быть заданы в одной из трех форм: infix (например, x + y); prefix (+xy); postfix (xy+). Последние две формы дают бесскобочную запись (скобки вводятся, в инфиксной форме, для явного указания порядка выполнения операций). Пример. Инфиксная (обычная) форма: a + b * c – (d – e / f). Префиксная форма (проход и запись выражения справа налево): + a – * bc – d / e f. Постфиксная форма (проход и запись слева направо), по-другому – это обратная (инверсная) польская запись (по имени польского математика Я. Лукасевича): a b c * + d e f / – –. Последняя форма (ОПЗ) широко используется в вычислительной технике, в частности при построении так называемых прямых трансляторов с языков программирования (используется стек с приоритетами). Бинарная операция удобно задается таблицей (табл. 1). Таблица 1 Операция на множестве M={a, b, c}
В дальнейшем будем говорить о некоторых замечательных свойствах операций, связывая эти свойства с фиксированными номерами (1, 2, …).
|