Пример. Можно считать функционал функцией с нетривиальной областью значений
тогда:
Можно считать функционал функцией с нетривиальной областью значений. Еще один специальный случай связан с отображением, сохраняющим эквивалентность. Пусть М – множество с r-отношением эквивалентности. Тогда М разбивается этим отношением на r-эквивалентные классы:
Итак, есть отношения эквивалентности rX и rY определенные соответственно на множествах X и Y, и есть отображение
Отображение f сохраняет эквивалентность, если f1 – функция, т.е.
Если же f1 – не функция, т.е. выходит за пределы класса эквивалентности (например, [х1]), то f – не сохраняет эквивалентность. В благоприятном же случае можно говорить: отображение f: X ® Y индуцирует отображение
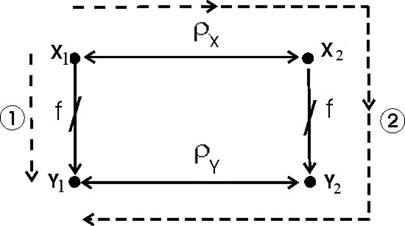
Рис. 2. Графическая интерпретация отображения f,
Видно, что существуют 2 пути от х1 к y1: 1: y1 = f(x1); 2: x1rX x2 ® y2 = f(x2) ® y2rY y1.
|
.
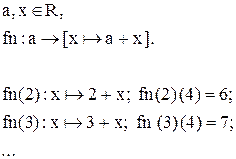
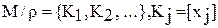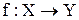. Есть еще межклассовые отношения: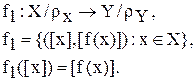
.
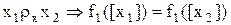(рис. 2).
