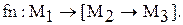Теорема
Любая подстановка на конечном множестве A (т.е. биективному подмножеству Nn) может быть представлена как произведение непересекающихся циклов. Действительно, начав слева, от 1 в верхней строке, формируем первый цикл по принципу «сверху вниз, снова вверх и т.д. до замыкания на начальное значение». На основе оставшихся элементов верхней строки формируем второй цикл и т.д. Поскольку множество А (или Nn) конечное, процесс рано или поздно останавливается. Теперь нужно показать еще непересекаемость циклов. Это следует, например, из условия неповторяемости элементов (в нижней, например, строке рис. 1).
Рис. 1. К непересекаемости циклов Доказательство от противного: пусть, наоборот, цикл 2 (H2, K2) вложен в цикл 1 (H1, K1). Тогда из-за обязательности равенств элементов на двойной стрелке (рис. 17) и K2 = H2 (замыкание) получаем в нижней строке запрещенное повторение элементов K2. На множестве М в отображении N ® M можно определить последовательность. Например,
Функционал – это функция, определенная на множестве не простых объектов (чисел), а на множестве тоже, например, функций:
Здесь после стрелки указано множество, например, всех функций из M2 в M3.
|