а) Отношения “  ” и “
” и “  ” являются отношениями нестрогого порядка, отношения “< ” и “> ” – отношениями строгого порядка (на всех основных числовых множествах). Оба отношения полностью упорядочивают множества
” являются отношениями нестрогого порядка, отношения “< ” и “> ” – отношениями строгого порядка (на всех основных числовых множествах). Оба отношения полностью упорядочивают множества 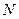 и
и  .
.
б) Определим отношения “  ” и “< ” на множестве
” и “< ” на множестве  следующим образом:
следующим образом:
1)  , если
, если 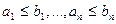 ;
;
2) 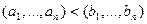 , если
, если  и при этом ходя бы для одной
и при этом ходя бы для одной  координаты выполняется
координаты выполняется  .
.
Тогда, например,  , но
, но  и
и  несравнимы. Таким образом, эти отношения частично упорядочивают
несравнимы. Таким образом, эти отношения частично упорядочивают  .,
.,
в) На системе подмножеств множества  отношение включения “
отношение включения “  ” задаёт нестрогий частичный порядок, а отношение строгого включения “
” задаёт нестрогий частичный порядок, а отношение строгого включения “  ” задаёт строгий частичный порядок. Например,
” задаёт строгий частичный порядок. Например,  , а
, а 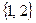 и
и  не сравнимы.
не сравнимы.
г) Отношение подчинённости в трудовом коллективе создаёт строгий частичный порядок. В нём, например, несравнимыми являются сотрудники различных структурных подразделений (отделов и т. п.).
д) В алфавите русского языка порядок букв зафиксирован, то есть всегда один и тот же. Тогда этот список определяет полное упорядочение букв, которое называется отношением предшествования. Обозначается  (
( предшествует
предшествует  ). На основании отношения предшествования букв построено отношение предшествования слов, определяемое примерно, таким образом, как производится сравнение двух десятичных дробей. Это отношение задаёт полное упорядочение слов в русском алфавите, которое называется лексикографическим упорядочением.
). На основании отношения предшествования букв построено отношение предшествования слов, определяемое примерно, таким образом, как производится сравнение двух десятичных дробей. Это отношение задаёт полное упорядочение слов в русском алфавите, которое называется лексикографическим упорядочением.

 ” и “
” и “  ” являются отношениями нестрогого порядка, отношения “< ” и “> ” – отношениями строгого порядка (на всех основных числовых множествах). Оба отношения полностью упорядочивают множества
” являются отношениями нестрогого порядка, отношения “< ” и “> ” – отношениями строгого порядка (на всех основных числовых множествах). Оба отношения полностью упорядочивают множества 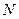 и
и  .
. следующим образом:
следующим образом: , если
, если 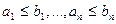 ;
;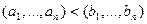 , если
, если  координаты выполняется
координаты выполняется  .
. , но
, но  и
и  несравнимы. Таким образом, эти отношения частично упорядочивают
несравнимы. Таким образом, эти отношения частично упорядочивают  отношение включения “
отношение включения “  ” задаёт нестрогий частичный порядок, а отношение строгого включения “
” задаёт нестрогий частичный порядок, а отношение строгого включения “  ” задаёт строгий частичный порядок. Например,
” задаёт строгий частичный порядок. Например,  , а
, а 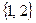 и
и  не сравнимы.
не сравнимы. (
( предшествует
предшествует  ). На основании отношения предшествования букв построено отношение предшествования слов, определяемое примерно, таким образом, как производится сравнение двух десятичных дробей. Это отношение задаёт полное упорядочение слов в русском алфавите, которое называется лексикографическим упорядочением.
). На основании отношения предшествования букв построено отношение предшествования слов, определяемое примерно, таким образом, как производится сравнение двух десятичных дробей. Это отношение задаёт полное упорядочение слов в русском алфавите, которое называется лексикографическим упорядочением.


