а) Отношение равенства (часто обозначается  ) на любом множестве является отношением эквивалентности. Равенство – это минимальное отношение эквивалентности в том смысле, что при удалении любой пары из этого отношения (то есть любой единицы на главной диагонали матрицы
) на любом множестве является отношением эквивалентности. Равенство – это минимальное отношение эквивалентности в том смысле, что при удалении любой пары из этого отношения (то есть любой единицы на главной диагонали матрицы  ) оно перестаёт быть рефлексивным и, следовательно, уже не является эквивалентностью.
) оно перестаёт быть рефлексивным и, следовательно, уже не является эквивалентностью.
б) Утверждения вида 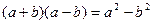 или
или  , состоящие из формул, соединённых знаком равенства, задают бинарное отношение на множестве формул, описывающих суперпозиции элементарных функций. Это отношение обычно называется отношением равносильности и определяется следующим образом: две формулы равносильны, если они задают одну и ту же функцию. Равносильность в данном случае, хотя и обозначена знаком “=”, означает не то же самое, что отношение равенства, так как оно может выполняться для различных формул. Впрочем, можно считать, что знак равенства в таких отношениях относится не к самим формулам, а к функциям, которые ими описываются. Для формул же отношение равенства – это совпадение формул по написанию. Оно называется графическим равенством. Кстати, чтобы в подобных ситуациях избежать разночтений, часто для обозначения отношения равносильности используют знак “
, состоящие из формул, соединённых знаком равенства, задают бинарное отношение на множестве формул, описывающих суперпозиции элементарных функций. Это отношение обычно называется отношением равносильности и определяется следующим образом: две формулы равносильны, если они задают одну и ту же функцию. Равносильность в данном случае, хотя и обозначена знаком “=”, означает не то же самое, что отношение равенства, так как оно может выполняться для различных формул. Впрочем, можно считать, что знак равенства в таких отношениях относится не к самим формулам, а к функциям, которые ими описываются. Для формул же отношение равенства – это совпадение формул по написанию. Оно называется графическим равенством. Кстати, чтобы в подобных ситуациях избежать разночтений, часто для обозначения отношения равносильности используют знак “  ”.
”.
в) Рассмотрим множество треугольников на координатной плоскости, считая, что треугольник задан, если даны координаты его вершин. Два треугольника будем считать равными (конгруэнтными), если при наложении они совпадают, то есть, переведены друг в друга с помощью некоторого перемещения. Равенство является отношением эквивалентности на множестве треугольников.
г) Отношение “иметь один и тот же остаток отделения на натуральное число  ” на множестве натуральных чисел является отношением эквивалентности.
” на множестве натуральных чисел является отношением эквивалентности.
е) Отношение “быть делителем” не является на множестве 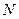 отношением эквивалентности. Оно обладает свойствами рефлексивности и транзитивности, но является антисимметричным (см. ниже).
отношением эквивалентности. Оно обладает свойствами рефлексивности и транзитивности, но является антисимметричным (см. ниже).
Пусть на множестве  задано отношение эквивалентности
задано отношение эквивалентности  . Осуществим следующее построение. Выберем элемент
. Осуществим следующее построение. Выберем элемент 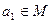 и образуем класс
и образуем класс 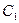 (подмножество
(подмножество  ), состоящий из элемента
), состоящий из элемента 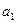 и всех элементов, эквивалентных ему в рамках данного отношения. Затем выберем элемент
и всех элементов, эквивалентных ему в рамках данного отношения. Затем выберем элемент  и образуем класс
и образуем класс  , состоящий из
, состоящий из 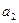 и эквивалентных ему элементов. Продолжая эти действия, получим систему классов
и эквивалентных ему элементов. Продолжая эти действия, получим систему классов  (возможно, бесконечную) такую, что любой элемент из множества
(возможно, бесконечную) такую, что любой элемент из множества  входит хотя бы в один класс, то есть
входит хотя бы в один класс, то есть 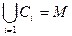 .
.
Эта система обладает следующими свойствами:
1) она образует разбиение множества  , то есть классы попарно не пересекаются;
, то есть классы попарно не пересекаются;
2) любые два элемента из одного класса эквивалентны;
3) любые два элемента из разных классов не эквивалентны.
Все эти свойства прямо следуют из определения отношения эквивалентности. Действительно, если бы, например, классы 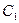 и
и  пресекались, то они имели бы хотя бы один общий элемент. Этот элемент был бы, очевидно, эквивалентен
пресекались, то они имели бы хотя бы один общий элемент. Этот элемент был бы, очевидно, эквивалентен 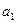 и
и 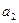 . Тогда, в силу транзитивности отношения
. Тогда, в силу транзитивности отношения  выполнялось бы
выполнялось бы  . Однако, по способу построения классов, это не возможно. Аналогично можно доказать другие два свойства.
. Однако, по способу построения классов, это не возможно. Аналогично можно доказать другие два свойства.
Построенное разбиение, то есть система классов – подмножеств множества  , называется системой классов эквивалентности по отношению
, называется системой классов эквивалентности по отношению  . Мощность этой системы называется индексом разбиения. С другой стороны, любое разбиение множества
. Мощность этой системы называется индексом разбиения. С другой стороны, любое разбиение множества  на классы само определяет некоторое отношение эквивалентности, а именно отношение “входить в один класс данного разбиения”.
на классы само определяет некоторое отношение эквивалентности, а именно отношение “входить в один класс данного разбиения”.

 ) на любом множестве является отношением эквивалентности. Равенство – это минимальное отношение эквивалентности в том смысле, что при удалении любой пары из этого отношения (то есть любой единицы на главной диагонали матрицы
) на любом множестве является отношением эквивалентности. Равенство – это минимальное отношение эквивалентности в том смысле, что при удалении любой пары из этого отношения (то есть любой единицы на главной диагонали матрицы  или
или  , состоящие из формул, соединённых знаком равенства, задают бинарное отношение на множестве формул, описывающих суперпозиции элементарных функций. Это отношение обычно называется отношением равносильности и определяется следующим образом: две формулы равносильны, если они задают одну и ту же функцию. Равносильность в данном случае, хотя и обозначена знаком “=”, означает не то же самое, что отношение равенства, так как оно может выполняться для различных формул. Впрочем, можно считать, что знак равенства в таких отношениях относится не к самим формулам, а к функциям, которые ими описываются. Для формул же отношение равенства – это совпадение формул по написанию. Оно называется графическим равенством. Кстати, чтобы в подобных ситуациях избежать разночтений, часто для обозначения отношения равносильности используют знак “
, состоящие из формул, соединённых знаком равенства, задают бинарное отношение на множестве формул, описывающих суперпозиции элементарных функций. Это отношение обычно называется отношением равносильности и определяется следующим образом: две формулы равносильны, если они задают одну и ту же функцию. Равносильность в данном случае, хотя и обозначена знаком “=”, означает не то же самое, что отношение равенства, так как оно может выполняться для различных формул. Впрочем, можно считать, что знак равенства в таких отношениях относится не к самим формулам, а к функциям, которые ими описываются. Для формул же отношение равенства – это совпадение формул по написанию. Оно называется графическим равенством. Кстати, чтобы в подобных ситуациях избежать разночтений, часто для обозначения отношения равносильности используют знак “  ”.
”. ” на множестве натуральных чисел является отношением эквивалентности.
” на множестве натуральных чисел является отношением эквивалентности.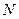 отношением эквивалентности. Оно обладает свойствами рефлексивности и транзитивности, но является антисимметричным (см. ниже).
отношением эквивалентности. Оно обладает свойствами рефлексивности и транзитивности, но является антисимметричным (см. ниже). задано отношение эквивалентности
задано отношение эквивалентности  . Осуществим следующее построение. Выберем элемент
. Осуществим следующее построение. Выберем элемент 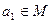 и образуем класс
и образуем класс 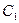 (подмножество
(подмножество 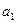 и всех элементов, эквивалентных ему в рамках данного отношения. Затем выберем элемент
и всех элементов, эквивалентных ему в рамках данного отношения. Затем выберем элемент  и образуем класс
и образуем класс  , состоящий из
, состоящий из 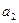 и эквивалентных ему элементов. Продолжая эти действия, получим систему классов
и эквивалентных ему элементов. Продолжая эти действия, получим систему классов  (возможно, бесконечную) такую, что любой элемент из множества
(возможно, бесконечную) такую, что любой элемент из множества 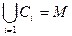 .
. . Однако, по способу построения классов, это не возможно. Аналогично можно доказать другие два свойства.
. Однако, по способу построения классов, это не возможно. Аналогично можно доказать другие два свойства.


