КванторыРассмотрим предложения: В любой треугольник можно вписать окружность. Всякое число, оканчивающееся на четную цифру, делится на 2. В этих предложениях встречаются слова «любой», «всякое». Эти слова заменяют специальным символом. Значок
( Например. Пусть Р (х) предикат, выражающий для х Наряду с квантором всеобщности в логике предикатов рассматривается квантор существования: Его значок ( Например. Пусть Р (х) предикат, выражающий для х Операция введения квантора называется операцией навешивания квантора. Навешивание квантора по какой-нибудь переменной понижает местность предиката. Переменная, по которой навешен квантор, называется связанной. Например. х< у - двухместный предикат. Навесим квантор: ( Таким образом, понизить местность предиката можно двумя способами. 1. задать предметной переменной конкретное значение. 2. навесить кванторы по одной или нескольким переменным. Квантор всеобщности можно рассматривать как обобщение конъюнкции для конечных и бесконечных множеств. Квантор существования можно рассматривать как обобщение дизъюнкции для конечных и бесконечных множеств.
|
называется квантором всеобщности.
U – запись, говорящая о том, что любой х из предметной области U обладает свойством Р.
.
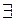х) (х 
